Zadanie nr 1685579
Jednym z miejsc zerowych funkcji kwadratowej 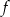 jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to
jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to 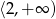 . Największa wartość funkcji
. Największa wartość funkcji 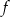 w przedziale
w przedziale 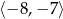 jest równa
jest równa 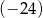 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 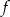 i narysuj jej wykres.
i narysuj jej wykres.
Rozwiązanie
Od początku myślmy sobie o wykresie funkcji 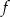 . Ponieważ ma ona być malejąca dokładnie na przedziale
. Ponieważ ma ona być malejąca dokładnie na przedziale 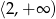 , wykres musi być parabolą o ramionach skierowanych w dół i wierzchołku w punkcie
, wykres musi być parabolą o ramionach skierowanych w dół i wierzchołku w punkcie 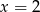 . Wiemy ponadto, że punkcie
. Wiemy ponadto, że punkcie 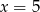 jest miejsce zerowe, co pozwala nam dość dokładnie naszkicować prawą połówkę paraboli (chociaż wciąż nie wiemy jaka dokładnie jest wartość funkcji w
jest miejsce zerowe, co pozwala nam dość dokładnie naszkicować prawą połówkę paraboli (chociaż wciąż nie wiemy jaka dokładnie jest wartość funkcji w 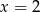 ).
).
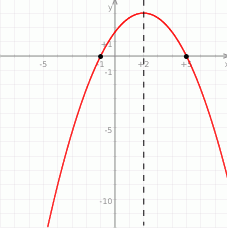
Ponieważ parabola jest symetryczna względem pionowej prostej przechodzącej przez wierzchołek, łatwo odgadnąć jakie jest jej drugie miejsce zerowe: jest to punkt położony symetrycznie do 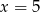 względem punktu
względem punktu 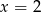 , czyli
, czyli 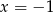 .
.
Z powyższej analizy wiemy, szukana funkcja ma wzór postaci
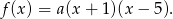
Pozostało wyliczyć  . Z naszkicowanego obrazka widać, że największa wartość
. Z naszkicowanego obrazka widać, że największa wartość 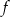 w przedziale
w przedziale 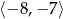 to
to 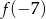 (bo funkcja jest w tym przedziale rosnąca). Mamy więc
(bo funkcja jest w tym przedziale rosnąca). Mamy więc
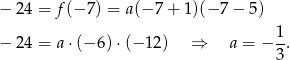
Zatem
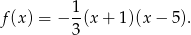
Odpowiedź: