Zadanie nr 2151885
Wielomiany 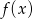 i
i 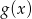 spełniają warunki
spełniają warunki 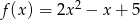 i
i 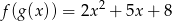 . Wyznacz wzór wielomianu
. Wyznacz wzór wielomianu 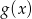 .
.
Rozwiązanie
Skoro po wstawieniu 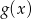 do wielomianu
do wielomianu 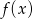 w miejsce
w miejsce  nadal mamy wielomian stopnia 2, wielomian
nadal mamy wielomian stopnia 2, wielomian 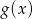 musi być stopnia 1, czyli szukamy wielomianu postaci
musi być stopnia 1, czyli szukamy wielomianu postaci 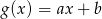 . Mamy zatem równanie
. Mamy zatem równanie
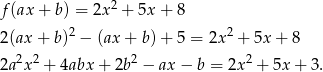
Dwa wielomiany są równe jeżeli mają równe współczynniki, więc
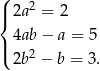
Z pierwszego równania mamy 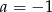 lub
lub 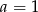 . Jeżeli
. Jeżeli 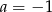 to z drugiego mamy
to z drugiego mamy

Jeżeli natomiast 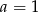 to
to
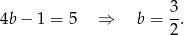
Łatwo sprawdzić, że w obu przypadkach spełnione jest trzecie równanie.
Odpowiedź: 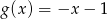 lub
lub