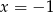/Szkoła średnia/Funkcje/Kwadratowa

Zadanie nr 2310185

Dodaj do ulubionych
Dodaj do rozwiązanych

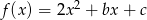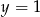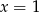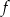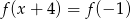Wiesz, że funkcja kwadratowa 2 f(x) = 2x + bx+ c przyjmuje wartość najmniejszą y = 1 dla x = 1 . Wyznacz wzór funkcji f , a następnie rozwiąż równanie f (x+ 4) = f(− 1) .

Rozwiązanie

Wykresem funkcji 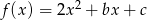2 f(x ) = 2x + bx + c jest parabola o ramionach skierowanych w górę, więc funkcja ta przyjmuje najmniejszą wartość w wierzchołku, czyli dla 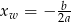xw = − -b 2a . Mamy stąd

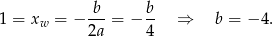
-b- b- 1 = xw = − 2a = − 4 ⇒ b = − 4.

Wartość najmniejsza to 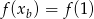f(xb) = f(1) , co pozwala obliczyć c .

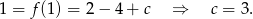
1 = f(1) = 2 − 4 + c ⇒ c = 3.

Zatem 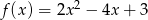f(x) = 2x2 − 4x + 3 i pozostało rozwiązać równanie

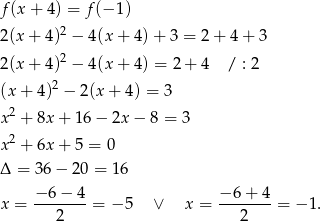
f(x + 4) = f(− 1) 2 2(x + 4) − 4(x + 4) + 3 = 2 + 4 + 3 2(x + 4)2 − 4(x + 4) = 2+ 4 / : 2 2 (x + 4) − 2(x + 4) = 3 x2 + 8x + 16 − 2x − 8 = 3 x2 + 6x + 5 = 0 Δ = 36 − 20 = 16 −-6−--4 −-6+--4 x = 2 = − 5 ∨ x = 2 = − 1.

 
Odpowiedź: 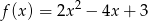f (x) = 2x2 − 4x + 3 , rozwiązania: 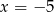x = − 5 i x = − 1

Wersja PDF