/Szkoła średnia/Funkcje/Kwadratowa

Zadanie nr 2893678

Zbiorem wartości funkcji kwadratowej 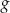g jest przedział 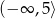(− ∞ ,5⟩ , a zbiorem rozwiązań nierówności 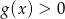g (x) > 0 jest przedział 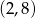(2,8) . Wyznacz wzór funkcji g .

Wersja PDF

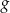Rozwiązanie

Informacja o zbiorze wartości oznacza, że wykresem funkcji 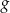g jest parabola o ramionach skierowanych w dół i wierzchołku, którego druga współrzędna jest równa 5.

Druga informacja oznacza natomiast, że miejscami zerowymi tej funkcji są liczby 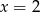x = 2 i x = 8 .

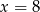Wierzchołek paraboli zawsze znajduje się dokładnie w środku między pierwiastkami (jeżeli istnieją), zatem

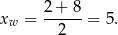
xw = 2+--8-= 5 . 2

Dalsze rozwiązanie przeprowadzimy na dwa sposoby.

Sposób I

Korzystając z postaci kanonicznej, szukamy funkcji i postaci

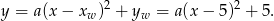
y = a(x− x )2 + y = a(x − 5)2 + 5. w w

Współczynnik a wyznaczamy sprawdzając, kiedy liczba 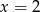x = 2 jest pierwiastkiem.

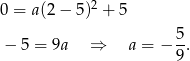
2 0 = a(2 − 5 ) + 5 5- − 5 = 9a ⇒ a = − 9.

Zatem szukana funkcja to

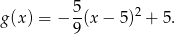
5- 2 g(x ) = − 9(x − 5) + 5.

Sposób II

Skoro znamy pierwiastki trójmianu, to wiemy, że jest ona postaci

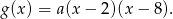
g(x ) = a(x − 2)(x − 8).

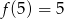Współczynnik a wyznaczamy sprawdzając, kiedy f(5) = 5 (bo są to współrzędne wierzchołka).

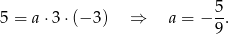
5 = a⋅3 ⋅(− 3) ⇒ a = − 5. 9

Zatem

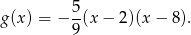
g(x) = − 5(x − 2)(x − 8). 9

 
Odpowiedź: g(x ) = − 59(x − 5)2 + 5 = − 59(x − 2 )(x − 8)

Wersja PDF