/Szkoła średnia/Funkcje/Kwadratowa

Zadanie nr 3456787

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest trójmian kwadratowy 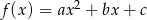2 f(x) = ax + bx+ c .

  • Dla 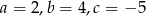a = 2,b = 4,c = − 5 wyznacz największą i najmniejszą wartość tego trójmianu w przedziale ⟨− 3,2⟩ .
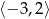  • Wyznacz wzór trójmianu w postaci iloczynowej, jeśli wiadomo, że ma on miejsca zerowe 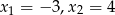x1 = − 3,x2 = 4 , a do jego wykresu należy punkt A = (2 ,−2 0) .

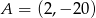Rozwiązanie

  • Dla podanych parametrów trójmian ma postać
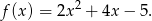
    f(x ) = 2x2 + 4x − 5.

    Wyznaczamy współrzędne 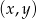(x,y) wierzchołka wykresu tego trójmianu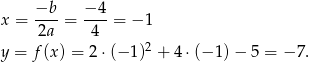

    −b-- −-4- x = 2a = 4 = − 1 2 y = f(x) = 2⋅(− 1) + 4 ⋅(− 1)− 5 = − 7.

    Ponieważ wykres funkcji 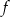f jest parabolą zwróconą ramionami do góry, więc najmniejszą wartość przyjmuje w wierzchołku. Ponieważ wierzchołek należy do przedziału, więc największą wartość funkcja przyjmie na jednym z końców przedziału. Liczymy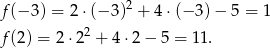

    f(− 3) = 2⋅(− 3)2 + 4 ⋅(− 3)− 5 = 1 2 f(2) = 2⋅2 + 4 ⋅2 − 5 = 11 .

    Zatem najmniejszą wartością jest -7, a największą 11.  
    Odpowiedź: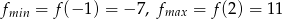 fmin = f(− 1 ) = − 7, fmax = f(2) = 11

  • Wielomian o pierwiastkach 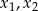x1,x2 ma postać iloczynową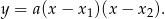
    y = a(x− x1)(x − x2).

    Podstawiamy współrzędne punktu 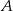A i wyznaczamy współczynnik a

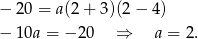
    − 20 = a(2 + 3)(2 − 4) − 10a = − 20 ⇒ a = 2.

    Zatem trójmian ma postać iloczynową

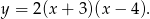
    y = 2(x + 3)(x − 4).

     
    Odpowiedź: f(x ) = 2(x + 3)(x − 4)

Wersja PDF