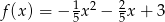Zadanie nr 4331106
Funkcja kwadratowa 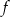 przyjmuje największą wartość równą
przyjmuje największą wartość równą 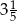 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 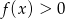 jest przedział
jest przedział 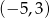 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 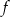 w postaci ogólnej.
w postaci ogólnej.
Rozwiązanie
Ponieważ rozwiązaniem nierówności 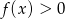 jest zbiór
jest zbiór 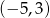 , więc wykres funkcji
, więc wykres funkcji 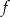 jest parabolą zwróconą gałęziami w dół, która przecina oś
jest parabolą zwróconą gałęziami w dół, która przecina oś 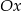 dla
dla 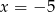 i
i 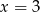 Zatem funkcja
Zatem funkcja 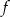 ma postać
ma postać
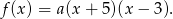
Ponieważ 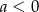 , więc największą wartość
, więc największą wartość 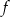 przyjmuje w wierzchołku. Wierzchołek paraboli znajduje się dokładnie w środku między pierwiastkami, więc
przyjmuje w wierzchołku. Wierzchołek paraboli znajduje się dokładnie w środku między pierwiastkami, więc 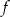 przyjmuje wartość największą dla
przyjmuje wartość największą dla
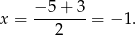
Stąd
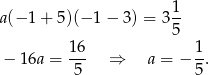
Pozostało nam tylko przekształcić wzór do postaci ogólnej
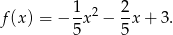
Odpowiedź: