Zadanie nr 5737884
W poniższej tabeli podane są wartości funkcji kwadratowej 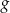 dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
| x | -2 | -1 | 0 | 1 | |
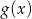 | -4 | 1 | 2 | -1 |
- Wyznacz wzór funkcji
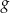 .
. - Uzupełnij brakujące zapisy w tabeli.
- Rozwiąż nierówność
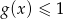 .
.
Rozwiązanie
- Szukamy funkcji w postaci
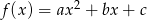 . Z podanych informacji wiemy, że
. Z podanych informacji wiemy, że 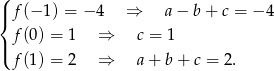
Dodając do pierwszego równania trzecie (żeby skrócić
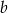 ) mamy
) mamy 
Zatem z pierwszego równania
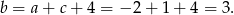
Odpowiedź: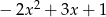
- W pierwszym brakującym miejscu wpisujemy
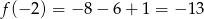 , a w drugim taką liczbę
, a w drugim taką liczbę 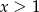 , dla której
, dla której 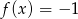 . Można tę liczbę ogadnąć lub rozwiązać równanie:
. Można tę liczbę ogadnąć lub rozwiązać równanie: 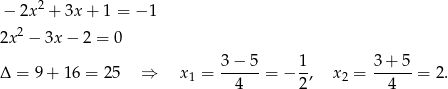
Zatem
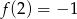 .
. x -2 -1 0 1 2 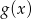
-13 -4 1 2 -1 - Liczymy
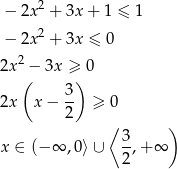
Odpowiedź: