/Szkoła średnia/Funkcje/Kwadratowa

Zadanie nr 6824145

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbadaj, na podstawie definicji, monotoniczność funkcji 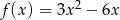2 f(x) = 3x − 6x w zbiorze (− ∞ ,1) .

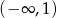Rozwiązanie

Funkcja jest odpowiednio rosnąca/malejąca, jeżeli

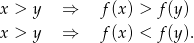
x > y ⇒ f (x) > f(y ) x > y ⇒ f (x) < f(y ).

Ustalmy 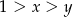1 > x > y i liczymy

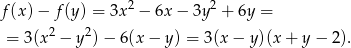
f(x )− f (y) = 3x2 − 6x − 3y 2 + 6y = 2 2 = 3(x − y ) − 6(x − y ) = 3(x − y)(x + y − 2).

Wyrażenie to jest ujemne (bo 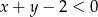x+ y− 2 < 0 ), więc funkcja jest malejąca.  
Odpowiedź: Malejąca

Wersja PDF