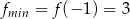/Szkoła średnia/Funkcje/Kwadratowa

Zadanie nr 6944676

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz najmniejszą i największą wartość funkcji 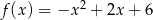2 f(x) = −x + 2x+ 6 w przedziale ⟨− 1,2 ⟩ .

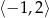Rozwiązanie

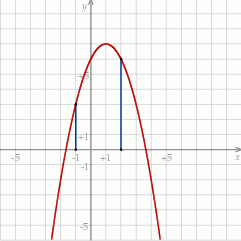
Widać, że wykres funkcji 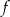f jest parabolą zwróconą ramionami w dół czyli, największą wartość przyjmuje w wierzchołku.

PIC

Najpierw sprawdzamy czy pierwsza współrzędna wierzchołka należy do przedziału 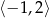⟨− 1,2⟩

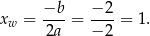
x = −b-= −-2-= 1. w 2a − 2

Zatem wierzchołek należy do interesującego nas przedziału, więc największą wartością w tym przedziale jest

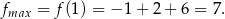
fmax = f(1) = −1 + 2 + 6 = 7.

Wartość najmniejszą otrzymamy w jednym z końców przedziału. W którym? – liczymy i sprawdzamy.

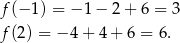
f(− 1) = − 1 − 2 + 6 = 3 f(2) = − 4 + 4 + 6 = 6.

 
Odpowiedź: 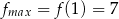fmax = f(1) = 7 , fmin = f(− 1) = 3

Wersja PDF