/Szkoła średnia/Funkcje/Kwadratowa

Zadanie nr 7349886

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz najmniejszą i największą wartość funkcji kwadratowej 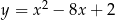2 y = x − 8x + 2 w przedziale ⟨3;7⟩ .

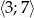Rozwiązanie

Sprawdźmy, czy wierzchołek paraboli będącej wykresem danej funkcji jest w danym przedziale.

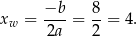
xw = −b-= 8-= 4. 2a 2

Wierzchołek jest wewnątrz interesującego nas przedziału, więc w nim funkcja przyjmuje wartość najmniejszą (bo ramiona paraboli są skierowane w górę) i jest ona równa

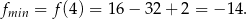
fmin = f(4 ) = 16− 32 + 2 = − 14.

Aby wyznaczyć wartość największą liczymy wartości w końcach przedziału.

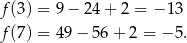
f(3 ) = 9− 24+ 2 = − 13 f(7 ) = 49− 56 + 2 = − 5.

Na koniec obrazek.

PIC

 
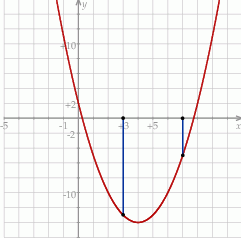
Odpowiedź: fmin = f (4) = − 14, fmax = f(7) = − 5

Wersja PDF