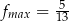/Szkoła średnia/Funkcje/Kwadratowa

Zadanie nr 8823356

Dodaj do ulubionych
Dodaj do rozwiązanych

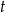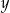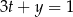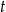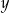Liczby rzeczywiste t i y spełniają warunek 3t+ y = 1 . Wyznacz takie wartości t i y , dla których wyrażenie 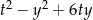t2 − y2 + 6ty przyjmuje największą wartość. Podaj tę największą wartość.

Rozwiązanie

Wiemy, że 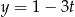y = 1− 3t , więc interesuje nas wartość wyrażenia

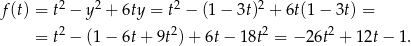
2 2 2 2 f(t) = t − y + 6ty = t − (1 − 3t) + 6t(1 − 3t) = = t2 − (1 − 6t + 9t2) + 6t− 18t2 = − 26t2 + 12t− 1.

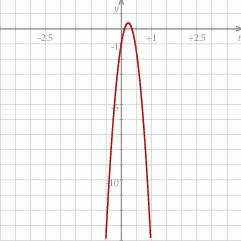
Wykresem tej funkcji jest parabola o ramionach skierowanych w dół i wierzchołku w punkcie

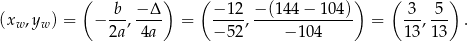
( b − Δ ) ( − 12 − (144− 104)) ( 3 5 ) (xw,yw ) = − --,---- = -----,-------------- = ---,--- . 2a 4a − 52 − 104 13 13

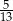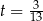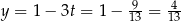W takim razie największa możliwa wartość danego wyrażenia to 5- 13 i otrzymamy ją dla 3- t = 13 i -9 4- y = 1 − 3t = 1 − 13 = 13 .

PIC

 
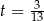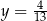Odpowiedź: t = 133 , y = 143 , fmax = 153

Wersja PDF