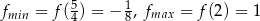/Szkoła średnia/Funkcje/Kwadratowa

Zadanie nr 9385103

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wartość największą i najmniejszą funkcji kwadratowej 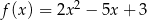f (x) = 2x2 − 5x + 3 w przedziale ⟨1,2⟩ .

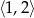Rozwiązanie

Wierzchołek paraboli będącej wykresem podanej funkcji kwadratowej jest w punkcie

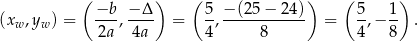
( ) ( ) ( ) (xw ,yw) = −b--, −-Δ = 5-, −-(25-−-24) = 5-,− 1- . 2a 4a 4 8 4 8

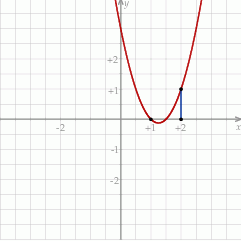
Punkt ten jest w podanym przedziale, więc najmniejsza wartość funkcji to 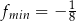fmin = − 1 8 (bo ramiona paraboli są skierowane do góry). Wartość największa to wartość w jednym z końców przedziału.

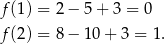
f(1) = 2 − 5 + 3 = 0 f(2) = 8 − 10 + 3 = 1.

Zatem 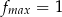fmax = 1 .

PIC

 
Odpowiedź: fmin = f (54) = − 18, fmax = f (2) = 1

Wersja PDF