Zadanie nr 9674445

Dana jest funkcja 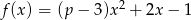2 f(x ) = (p − 3)x + 2x − 1 . Wyznacz te wartości parametru 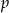, dla których:

największa wartość funkcji 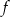jest liczbą ujemną,
najmniejsza wartość funkcji 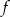jest mniejsza od -2.

Rozwiązanie

Na początku sprawdźmy przypadek gdy podana funkcja nie jest funkcją kwadratową, czyli dla 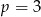p = 3 . Wtedy 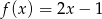f(x) = 2x − 1 i funkcja ta nie przyjmuje ani wartości najmniejszej ani największej.

Ponieważ funkcja ma przyjmować wartość największą więc jej ramiona muszą być skierowane w dół, czyli 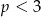. Ponadto mamy mieć 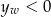, czyli funkcja nie może przecinać osi 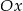. Zatem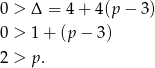
$0 > Δ = 4 + 4(p − 3) 0 > 1 + (p − 3) 2 > p .$

Odpowiedź: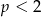
Podobnie jak poprzednio, ale tym razem funkcja ma osiągać minimum, czyli 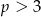. Ponadto musi być 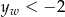, czyli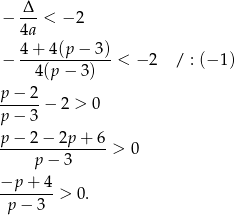
$− -Δ-< − 2 4a 4 + 4(p − 3) − ------------- < − 2 / : (− 1) 4(p − 3) p−--2- p− 3 − 2 > 0 p−--2−--2p-+-6-> 0 p − 3 −p + 4 --------> 0. p− 3$

Ponieważ mianownik tego ułamka jest dodatni (założyliśmy to), to mamy 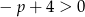, czyli .
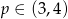Odpowiedź: