/Szkoła średnia/Ciągi/Geometryczny/Różne

Zadanie nr 2111650

Dodaj do ulubionych
Dodaj do rozwiązanych

W nieskończonym ciągu geometrycznym 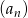(an ) o wyrazach dodatnich każdy wyraz począwszy od trzeciego, jest sumą dwóch poprzednich wyrazów. Oblicz iloraz tego ciągu.

Rozwiązanie

Jeżeli oznaczymy trzy pierwsze wyrazy ciągu przez 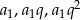2 a1,a1q,a1q to mamy równanie

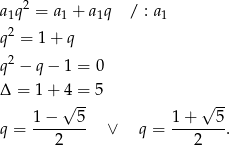
2 a1q = a1 + a 1q / : a1 q2 = 1 + q q2 − q − 1 = 0 Δ = 1 + 4 = 5 √ -- √ -- 1− 5 1+ 5 q = ---2---- ∨ q = ---2---.

Ponieważ ciąg ma mieć wyrazy dodatnie, musi być 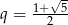√ - q = 1+--5 2 .  
Odpowiedź: 1+ √5 --2--

Wersja PDF