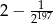/Szkoła średnia/Ciągi/Geometryczny/Różne

Zadanie nr 2171088

Dodaj do ulubionych
Dodaj do rozwiązanych

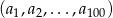Ciąg (a1,a2,...,a100) jest ciągiem geometrycznym o ilorazie 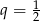1 q = 2 i pierwszym wyrazie równym 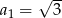√ -- a1 = 3 . Oblicz sumę

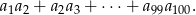
a1a2 + a 2a3 + ⋅⋅ ⋅+ a99a100.

Rozwiązanie

Korzystamy ze wzoru 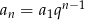n−1 an = a 1q na n -ty wyraz ciągu geometrycznego.

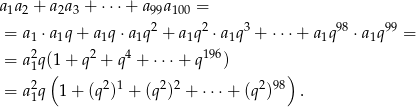
a a + a a + ⋅⋅⋅ + a a = 1 2 2 3 99 100 = a1 ⋅a1q + a1q ⋅a1q2 + a1q2 ⋅a1q3 + ⋅⋅⋅+ a1q 98 ⋅a1q99 = 2 2 4 196 = a1q((1+ q + q + ⋅ ⋅⋅+ q ) ) 2 2 1 2 2 2 98 = a1q 1+ (q ) + (q ) + ⋅⋅⋅+ (q ) .

W nawiasie mamy sumę 99 wyrazów ciągu geometrycznego o ilorazie 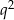q2 . Zatem ze wzoru na sumę kolejnych wyrazów ciągu geometrycznego mamy

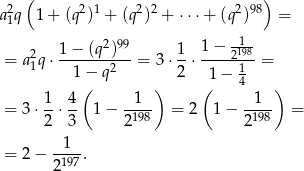
( ) 2 2 1 2 2 2 98 a1q 1 + (q ) + (q ) + ⋅⋅⋅+ (q ) = 2 99 1− -1- = a2q ⋅ 1-−-(q-)- = 3 ⋅ 1-⋅----2198-= 1 1 − q2 2 1− 14 ( ) ( ) = 3 ⋅ 1-⋅ 4 1 − -1-- = 2 1 − -1-- = 2 3 2198 2198 1 = 2 − --197. 2

 
Odpowiedź: -1- 2 − 2197

Wersja PDF