Zadanie nr 3702618
Oblicz iloczyn pierwszych 99 wyrazów ciągu geometrycznego 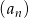 , w którym
, w którym 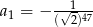 oraz
oraz 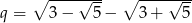 . Czy iloczyn ten jest liczbą wymierną?
. Czy iloczyn ten jest liczbą wymierną?
Rozwiązanie
Na razie nie przejmujmy się dziwacznymi wartościami 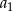 i
i 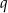 i policzmy iloczyn pierwszych 99 wyrazów ciągu
i policzmy iloczyn pierwszych 99 wyrazów ciągu 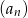 . Ze wzoru na
. Ze wzoru na  -ty wyraz ciągu geometrycznego mamy
-ty wyraz ciągu geometrycznego mamy
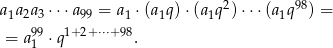
Zanim przekształcimy to wyrażenie dalej obliczmy sumę wykładników przy ilorazie 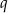 .
.
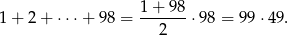
Zatem
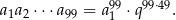
Teraz nie mamy wyjścia, musimy się przyjrzeć dokładniej liczbie 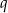 . Jest jasne, że
. Jest jasne, że 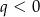 (bo
(bo 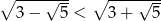 ), oraz
), oraz
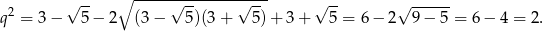
Zatem 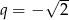 . Stąd
. Stąd
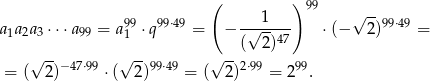
Oczywiście jest to liczba wymierna.
Odpowiedź: Tak, jest to liczba wymierna: