/Szkoła średnia/Ciągi/Geometryczny/Różne

Zadanie nr 5251444

Dodaj do ulubionych
Dodaj do rozwiązanych

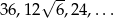Ciąg √ -- 36,12 6,24,... jest ciągiem geometrycznym.

  • Oblicz iloraz 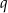q tego ciągu.
  • Zapisz n -ty wyraz tego ciągu w postaci aqn
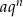
  • Oblicz sumę ośmiu początkowych wyrazów tego ciągu.

Rozwiązanie

  • Wystrczy podzielić dwa sąsiednie wyrazy przez siebie
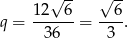
    √ -- √ -- q = 12---6 = --6-. 36 3
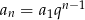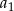  • Wzór na n -ty wyraz ciągu geometrycznego to a = a qn− 1 n 1 , gdzie a1 – pierwszy wyraz. Zatem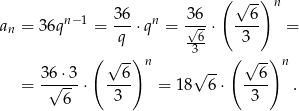
    ( √ --)n n−1 36- n -36 --6- an = 3 6q = q ⋅q = √6-⋅ 3 = ( ) 3 ( ) 36⋅ 3 √ 6- n √ -- √ 6- n = -√---⋅ ---- = 18 6⋅ ---- . 6 3 3
  • Ze wzoru na sumę ciągu geometrycznego mamy
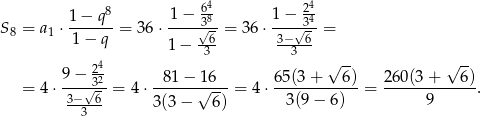
    4 4 1-−-q8- 1-−-638- 1−--234- S8 = a1 ⋅1 − q = 3 6⋅ √6-= 36⋅ 3−-√6- = 1− 3 3 24 √ -- √ -- = 4 ⋅ 9-−√32-= 4⋅ -81-−-1√6---= 4 ⋅ 65(3-+--6-)= 260-(3+----6). 3−--6 3(3− 6) 3(9− 6) 9 3

     
    Odpowiedź: √ - S = 260(3+--6) 8 9

Wersja PDF