/Szkoła średnia/Ciągi/Geometryczny/Różne

Zadanie nr 6493246

Dany jest ciąg geometryczny, w którym 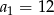a1 = 12 i a3 = 27 .

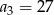  • Ile jest ciągów spełniających podane warunki? Odpowiedź uzasadnij.
  • Oblicz wyraz 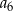a 6 tego ciągu, który jest rosnący. Wynik podaj w postaci ułamka dziesiętnego.
Wersja PDF

Rozwiązanie

  • Jeżeli przez 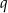q oznaczymy iloraz ciągu 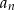an , to mamy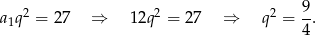
    a q2 = 27 ⇒ 12q2 = 27 ⇒ q2 = 9-. 1 4

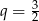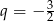    Zatem q = 3 2 lub q = − 3 2 i są dwa ciągi spełniające warunki zadania: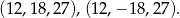

    (12,18 ,27),(12,− 18,27).

     
    Odpowiedź: Są dwa ciągi

  • Mamy
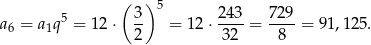
    ( 3) 5 243 729 a6 = a1q 5 = 12⋅ -- = 12⋅ ----= ----= 91,125. 2 3 2 8

     
    Odpowiedź: 91,125

Wersja PDF