/Szkoła średnia/Ciągi/Geometryczny/Różne

Zadanie nr 6495224

Kolejne cyfry dodatniej liczby trzycyfrowej tworzą ciąg geometryczny. Suma cyfr jedności i dziesiątek jest o jeden większa od cyfry setek. Jeżeli od szukanej liczby odejmiemy liczbę złożoną z tych samych cyfr, lecz napisanych w odwrotnej kolejności to otrzymamy 495. Znajdź tę liczbę.

Wersja PDF

Rozwiązanie

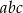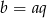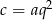Szukamy liczby o zapisie dziesiętnym postaci: abc , gdzie b = aq i 2 c = aq . Wiemy ponadto, że

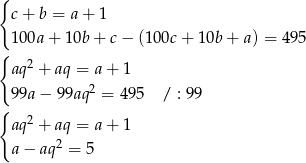
{ c+ b = a+ 1 100a + 10b + c − (100c + 10b + a) = 495 { aq2 + aq = a + 1 2 99a− 99aq = 4 95 / : 99 { 2 aq + aq = a + 1 a− aq2 = 5

Jeżeli dodamy równania układu stronami to mamy 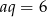aq = 6 , czyli 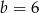b = 6 . Zauważmy, że drugie równanie układu, czyli 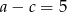a− c = 5 oznacza, że 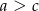a > c , czyli 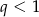q < 1 . To z kolei oznacza, że 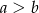a > b , czyli a może być równe 7, 8 lub 9. Wtedy c jest równe odpowiednio 2, 3 i 4. Sprawdzając kolejne liczby: 762, 863 i 964 stwierdzamy, że tylko liczba 964 spełnia warunki zadania.  
Odpowiedź: 964

Wersja PDF