/Szkoła średnia/Ciągi/Geometryczny/Różne

Zadanie nr 6829430

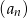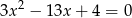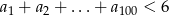Pierwszy wyraz i iloraz nieskończonego ciągu geometrycznego malejącego (an) są różnymi pierwiastkami równania 3x 2 − 13x + 4 = 0 . Sprawdź czy prawdziwa jest nierówność a1 + a2 + ...+ a100 < 6 .

Wersja PDF

Rozwiązanie

Rozwiązujemy podane równanie.

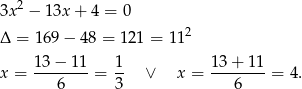
2 3x − 1 3x+ 4 = 0 Δ = 169 − 48 = 121 = 1 12 x = 13-−-11-= 1- ∨ x = 13-+-11-= 4. 6 3 6

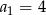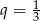Zatem a1 = 4 i 1 q = 3 . Liczymy sumę 100 początkowych wyrazów.

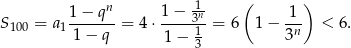
n -1 ( ) S = a 1-−-q--= 4 ⋅ 1-−-3n-= 6 1− 1-- < 6. 100 1 1 − q 1 − 1 3n 3

 
Odpowiedź: Nierówność jest prawdziwa.

Wersja PDF