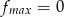Zadanie nr 9428758
Ciąg 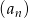 , gdzie
, gdzie 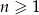 , jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji
, jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji 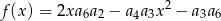 .
.
Rozwiązanie
Ze wzoru na  -ty wyraz ciągu geometrycznego mamy
-ty wyraz ciągu geometrycznego mamy
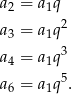
Korzystając z tych równości możemy wzór danej funkcji zapisać w postaci
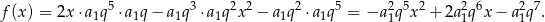
Sposób I
Funkcja 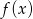 jest funkcją kwadratową o ramionach skierowanych w dół (tu korzystamy z tego, że ciąg jest rosnący!), więc przyjmuje wartość największą w wierzchołku. Sprawdźmy jaka jest pierwsza współrzędna wierzchołka.
jest funkcją kwadratową o ramionach skierowanych w dół (tu korzystamy z tego, że ciąg jest rosnący!), więc przyjmuje wartość największą w wierzchołku. Sprawdźmy jaka jest pierwsza współrzędna wierzchołka.
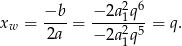
Zatem wartość największa jest równa
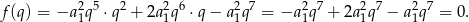
Sposób II
Zauważmy, że
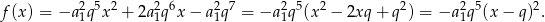
Ponieważ z założenia 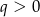 , więc największą możliwą wartością powyższego wyrażenia jest
, więc największą możliwą wartością powyższego wyrażenia jest
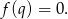
Odpowiedź: