/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez sumę

Zadanie nr 2070435

W ciągu arytmetycznym o nieparzystej liczbie wyrazów suma wyrazów stojących na miejscach nieparzystych równa się 44, a suma pozostałych wynosi 33. Znajdź wyraz środkowy i liczbę wyrazów tego ciągu.

Wersja PDF

Rozwiązanie

Jeżeli oznaczymy wyrazy ciągu przez 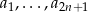a1,...,a2n+1 , to środkowy wyraz to 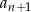an+ 1 (bo np. 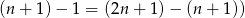(n + 1) − 1 = (2n + 1)− (n+ 1)) . Wiemy, że

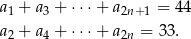
a1 + a3 + ⋅⋅⋅+ a2n+ 1 = 44 a2 + a4 + ⋅⋅⋅+ a2n = 33.

Sposób I

Z definicji ciągu arytmetycznego mamy

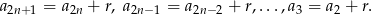
a = a + r, a = a + r,...,a = a + r. 2n+ 1 2n 2n− 1 2n−2 3 2

Zatem mamy

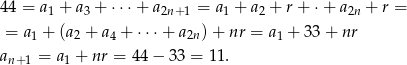
44 = a1 + a 3 + ⋅⋅⋅ + a2n+1 = a1 + a2 + r + ⋅+ a 2n + r = = a1 + (a2 + a4 + ⋅⋅⋅+ a2n)+ nr = a1 + 33+ nr an+ 1 = a1 + nr = 44 − 33 = 11.

Zauważmy, że

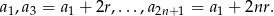
a ,a = a + 2r,...,a = a + 2nr. 1 3 1 2n+ 1 1

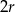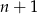jest ciągiem arytmetycznym o różnicy 2r i n+ 1 wyrazach. Ze wzoru na sumę takiego ciągu mamy.

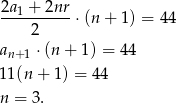
2a1 + 2nr ----------⋅(n + 1 ) = 44 2 an+1 ⋅(n + 1) = 4 4 11(n + 1) = 44 n = 3 .

Zatem wszystkich wyrazów jest 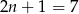2n + 1 = 7 .

Sposób II

Jak w sposobie pierwszym zauważamy, że ciąg

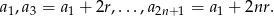
a1,a3 = a 1 + 2r,...,a2n+ 1 = a1 + 2nr.

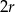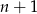jest ciągiem arytmetycznym o różnicy 2r i n + 1 wyrazach. Podobnie ciąg

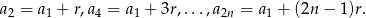
a2 = a1 + r,a4 = a1 + 3r,...,a2n = a1 + (2n − 1 )r.

jest ciągiem arytmetycznym o pierwszym wyrazie 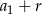a1 + r , różnicy 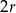2r i n wyrazach. Ze wzoru na sumę takiego ciągu mamy.

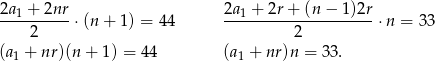
2a + 2nr 2a + 2r + (n − 1)2r ---1------⋅ (n+ 1) = 44 --1------------------⋅n = 33 2 2 (a1 + nr)(n + 1) = 44 (a1 + nr)n = 3 3.

Odejmując te dwie równości stronami, mamy

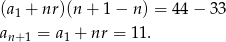
(a + nr )(n+ 1− n) = 44 − 33 1 an +1 = a1 + nr = 1 1.

Ponadto

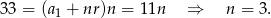
3 3 = (a1 + nr)n = 11n ⇒ n = 3.

 
Odpowiedź: Środkowy wyraz: 11, liczba wyrazów: 7.

Wersja PDF