/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez sumę

Zadanie nr 3458998

Dodaj do ulubionych
Dodaj do rozwiązanych

W ciągu arytmetycznym 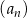(an) , określonym dla liczb naturalnych 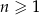n ≥ 1 , wyraz piąty jest liczbą trzy razy mniejszą od wyrazu szóstego, a suma dwunastu początkowych wyrazów tego ciągu jest równa 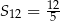S12 = 125 . Oblicz wyraz pierwszy oraz różnicę tego ciągu.

Rozwiązanie

Ze wzoru na n –ty wyraz ciągu arytmetycznego mamy

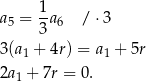
1 a5 = --a6 / ⋅3 3 3(a1 + 4r) = a1 + 5r 2a + 7r = 0. 1

Korzystamy teraz ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego.

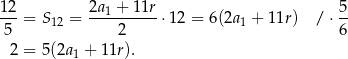
12 2a + 11r 5 ---= S12 = ---1------⋅12 = 6(2a1 + 11r) / ⋅ -- 5 2 6 2 = 5(2a1 + 11r).

Podstawiamy teraz w tej równości 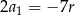2a 1 = − 7r .

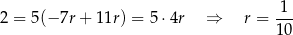
2 = 5(− 7r + 11r) = 5 ⋅4r ⇒ r = 1-- 10

Stąd

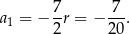
a1 = − 7-r = − 7-. 2 20

 
Odpowiedź: r = 110; a1 = − 270

Wersja PDF