Zadanie nr 3946885
Dany jest ciąg 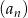 , w którym suma
, w którym suma  początkowych wyrazów wyraża się wzorem
początkowych wyrazów wyraża się wzorem 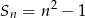 ,
, 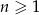 . Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
. Wyznacz wzór ogólny ciągu. Czy jest to ciąg arytmetyczny?
Rozwiązanie
Znając wzór sumę wyrazów, możemy wyznaczyć wzór ciągu 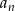 z równości
z równości
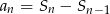
(sumy z prawej strony różnią się dokładnie o 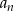 ). Wzór ten nie działa dla
). Wzór ten nie działa dla 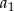 , ale
, ale 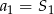 .
.
Liczymy.
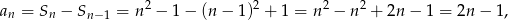
o ile 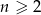 . Ponadto
. Ponadto 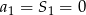 . Sprawdźmy czy jest to ciąg arytmetyczny
. Sprawdźmy czy jest to ciąg arytmetyczny
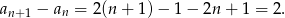
Ciąg wygląda zatem na ciąg arytmetyczny o różnicy 2. Nie jesteśmy jednak tego jeszcze pewni, bo nie sprawdziliśmy 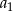 . Ponieważ
. Ponieważ 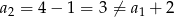 , więc nie jest to ciąg arytmetyczny.
, więc nie jest to ciąg arytmetyczny.
Odpowiedź: 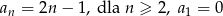 , nie jest arytmetyczny.
, nie jest arytmetyczny.

