/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez sumę

Zadanie nr 3954567

Dany jest ciąg arytmetyczny 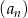(an ) określony dla każdej liczby naturalnej 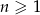n ≥ 1 , w którym suma pierwszych 50 wyrazów jest równa 9 900, a suma wyrazów o numerach od 41 do 70 (włącznie) jest równa 540. Oblicz sumę wszystkich dodatnich wyrazów tego ciągu.

Wersja PDF

Rozwiązanie

Korzystamy ze wzoru

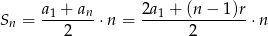
a + a 2a + (n − 1)r Sn = -1----n-⋅n = --1------------⋅n 2 2

na sumę n początkowych wyrazów ciągu arytmetycznego. Mamy zatem

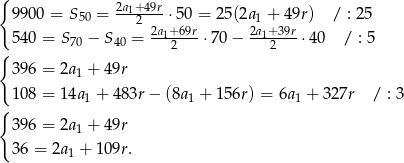
{ 2a1+49r 9900 = S50 = ---2---⋅5 0 = 25(2a1 + 49r) / : 25 540 = S70 − S40 = 2a1+69r⋅70 − 2a1+39r-⋅40 / : 5 { 2 2 396 = 2a1 + 49r { 108 = 14a1 + 483r − (8a1 + 156r) = 6a 1 + 3 27r / : 3 396 = 2a + 49r 1 36 = 2a1 + 109r.

Odejmujemy od drugiego równania pierwsze i mamy

60r = −3 60 ⇒ r = − 6.

Z drugiego równania

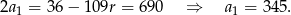
2a1 = 3 6− 109r = 690 ⇒ a1 = 345.

Stąd

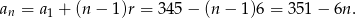
an = a + (n − 1)r = 34 5− (n − 1)6 = 351 − 6n . 1

Sprawdzamy teraz, które wyrazy ciągu 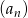(a ) n są dodatnie.

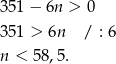
351 − 6n > 0 351 > 6n / : 6 n < 58,5.

W takim razie pierwsze 58 wyrazów ciągu 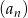(an) jest dodatnich. Obliczamy ich sumę

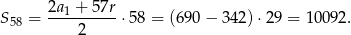
2a 1 + 5 7r S58 = -----2----⋅ 58 = (690 − 342 )⋅29 = 10092.

 
Odpowiedź: 10092

Wersja PDF