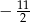/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez sumę

Zadanie nr 6091371

Dziesiąty wyraz ciągu arytmetycznego 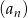(an) jest o 48 mniejszy od sumy jego pierwszych 7 wyrazów. Oblicz sumę pierwszych 33 wyrazów tego ciągu wiedząc, że iloczyn 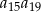a15a 19 ma najmniejszą możliwą wartość.

Wersja PDF

Rozwiązanie

Jeżeli r jest różnicą danego ciągu to wiemy, że

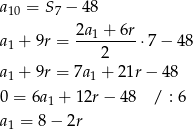
a = S − 48 10 7 2a1-+-6r- a1 + 9r = 2 ⋅7 − 48 a + 9r = 7a + 21r − 48 1 1 0 = 6a1 + 12r − 48 / : 6 a1 = 8 − 2r

W takim razie iloczyn 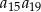a15a 19 jest równy

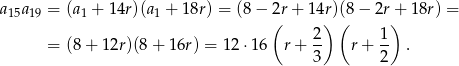
a15a 19 = (a1 + 1 4r)(a1 + 1 8r) = (8− 2r+ 14r)(8− 2r+ 18r) = ( ) ( ) = (8+ 1 2r)(8+ 16r) = 12 ⋅16 r + 2- r + 1- . 3 2

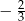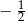Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę i miejscach zerowych 2 − 3 oraz 1 − 2 . W takim razie to wyrażenie będzie miało najmniejszą możliwą wartość w wierzchołku paraboli, czyli dokładnie w środku między pierwiastkami. Zatem

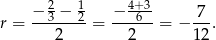
− 23 − 12 − 4+63- 7 r = --------= ------= − --. 2 2 12

Wtedy

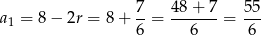
7 4 8+ 7 55 a1 = 8 − 2r = 8+ --= ------- = --- 6 6 6

i suma początkowych 33 wyrazów jest równa

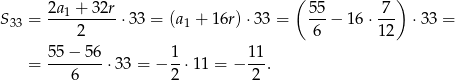
( ) 2a 1 + 32r 55 7 S33 = ----------⋅3 3 = (a1 + 16r)⋅ 33 = ---− 16 ⋅--- ⋅33 = 2 6 1 2 55-−-5-6 1- 11- = 6 ⋅ 33 = − 2 ⋅11 = − 2 .

 
Odpowiedź: 11 − 2

Wersja PDF