/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez sumę

Zadanie nr 7463208

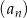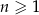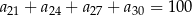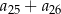Dany jest ciąg arytmetyczny (an ) , określony dla n ≥ 1 , w którym spełniona jest równość a21 + a24 + a27 + a30 = 100 . Oblicz sumę a25 + a 26 .

Wersja PDF

Rozwiązanie

Sposób I

Korzystamy ze wzoru 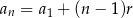an = a1 + (n − 1)r na n –ty wyraz ciągu arytmetycznego.

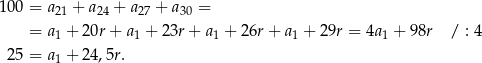
100 = a + a + a + a = 21 24 27 30 = a1 + 20r + a1 + 23r + a1 + 26r + a1 + 29r = 4a1 + 98r / : 4 25 = a + 24,5r. 1

W takim razie

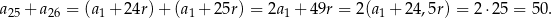
a25+ a26 = (a1 + 24r)+ (a1+ 25r ) = 2a1+ 4 9r = 2(a1+ 24,5r) = 2 ⋅25 = 50.

Sposób II

Jeżeli oznaczymy przez r różnicę ciągu 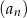(an) , to

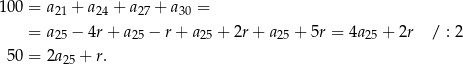
100 = a + a + a + a = 21 24 27 30 = a25 − 4r + a25 − r+ a25 + 2r + a25 + 5r = 4a25 + 2r / : 2 50 = 2a + r. 25

Stąd

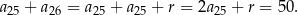
a25 + a26 = a25 + a25 + r = 2a25 + r = 50.

 
Odpowiedź: 50

Wersja PDF