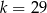/Szkoła średnia/Ciągi/Arytmetyczny/Dany przez sumę

Zadanie nr 7502418

Ciąg arytmetyczny 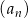(an) jest określony dla każdej liczby naturalnej 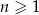n ≥ 1 . Różnicą tego ciągu jest liczba 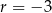r = − 3 , a średnia arytmetyczna początkowych siedmiu wyrazów tego ciągu: 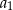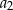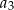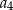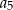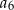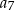a1 , a2 , a3 , a4 , a5 , a6 , a 7 , jest równa − 28 .

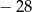  • Oblicz pierwszy wyraz tego ciągu.
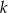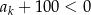  • Wyznacz najmniejszą liczbę k , dla której ak + 100 < 0 .
Wersja PDF

Rozwiązanie

  • Wiemy, że
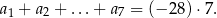
    a1 + a 2 + ...+ a7 = (− 28) ⋅7.

    Ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego, mamy więc

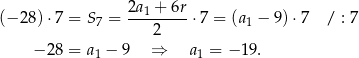
    2a1 +-6r- (− 28)⋅ 7 = S7 = 2 ⋅7 = (a1 − 9)⋅7 / : 7 −2 8 = a1 − 9 ⇒ a1 = − 19.

     
    Odpowiedź: a = − 19 1

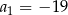
  • Ze wzoru na n –ty wyraz ciągu arytmetycznego, mamy nierówność
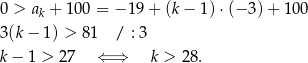
    0 > ak + 1 00 = − 19 + (k − 1)⋅ (−3 )+ 1 00 3(k − 1) > 81 / : 3 k − 1 > 2 7 ⇐ ⇒ k > 28 .

     
    Odpowiedź: k = 29

Wersja PDF