Zadanie nr 8231898
Ciąg 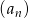 jest ciągiem arytmetycznym o pierwszym wyrazie równym 123 i różnicy będącej liczbą całkowitą. Ciąg
jest ciągiem arytmetycznym o pierwszym wyrazie równym 123 i różnicy będącej liczbą całkowitą. Ciąg 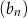 jest określony wzorem
jest określony wzorem 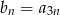 , dla
, dla 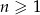 , oraz wiadomo, że suma pewnych
, oraz wiadomo, że suma pewnych 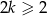 początkowych wyrazów ciągu
początkowych wyrazów ciągu 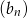 jest równa sumie
jest równa sumie 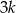 początkowych wyrazów ciągu
początkowych wyrazów ciągu 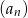 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 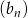 .
.
Rozwiązanie
Wiemy, że
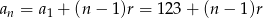
oraz
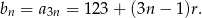
Zapiszmy teraz podaną informację o sumach początkowych wyrazów obu ciągów.
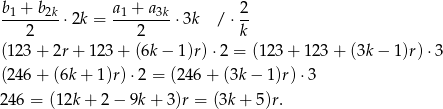
Zauważmy teraz, że założeń zadania obie liczby 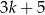 i
i  z prawej strony tej równości są całkowite, więc
z prawej strony tej równości są całkowite, więc 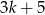 musi być dzielnikiem liczby
musi być dzielnikiem liczby
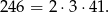
Łatwo sprawdzić, że liczba ta ma tylko dwa dzielniki tej postaci: 2 i 41. Ponieważ jednak 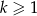 , pierwszą możliwość odrzucamy. Zatem
, pierwszą możliwość odrzucamy. Zatem

i 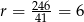 . Ciąg
. Ciąg 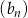 ma więc wzór
ma więc wzór
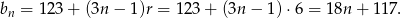
Odpowiedź: 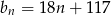 , dla
, dla 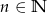 .
.

