/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt

Zadanie nr 2848484

Dodaj do ulubionych
Dodaj do rozwiązanych

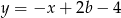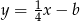Dane są proste o równaniach y = −x + 2b− 4 oraz 1 y = 4x − b , które przecinają się w punkcie leżącym na osi 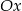Ox układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi Oy .

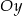Rozwiązanie

Sprawdźmy w jakich punktach podane proste przecinają oś 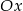Ox .

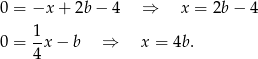
0 = −x + 2b− 4 ⇒ x = 2b − 4 1- 0 = 4x − b ⇒ x = 4b.

Wiemy, że proste te przecinają oś 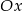Ox w tym samym punkcie, więc

2b − 4 = 4b ⇒ b = − 2

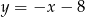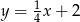i dane proste mają równania: y = −x − 8 i y = 14x+ 2 .

Możemy teraz naszkicować opisaną sytuację.

PIC

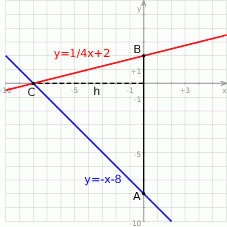
Pole trójkąta 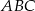ABC jest więc równe

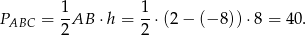
PABC = 1-AB ⋅h = 1-⋅(2 − (− 8)) ⋅8 = 40. 2 2

 
Odpowiedź: 40

Wersja PDF