Zadanie nr 3150459
W trójkąt równoboczny 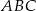 wpisano okrąg o środku w punkcie
wpisano okrąg o środku w punkcie 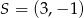 . Wiedząc, że wierzchołek
. Wiedząc, że wierzchołek 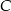 ma współrzędne
ma współrzędne 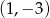 wyznacz współrzędne pozostałych wierzchołków tego trójkąta.
wyznacz współrzędne pozostałych wierzchołków tego trójkąta.
Rozwiązanie
Jak zwykle w geometrii najważniejszy jest rysunek.
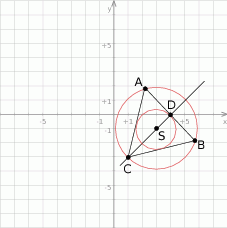
Sposób I
Jak już mamy rysunek, należy się zastanowić jak z podanych danych odtworzyć trójkąt? No dobrze, a co dokładnie mamy dane? Mając punkty 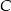 i
i 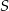 możemy wyliczyć równanie prostej
możemy wyliczyć równanie prostej 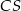 . Jak to mamy, to możemy wyliczyć spodek wysykości
. Jak to mamy, to możemy wyliczyć spodek wysykości 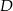 opuszczonej z wierzchołka
opuszczonej z wierzchołka 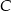 (bo wiemy, że leży na prostej
(bo wiemy, że leży na prostej 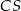 i jest w odległości
i jest w odległości 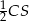 od
od 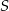 ). Potem będziemy mogli wyliczyć równanie prostej
). Potem będziemy mogli wyliczyć równanie prostej 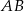 (bo jest prostopadła do
(bo jest prostopadła do 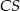 i przechodzi przez
i przechodzi przez 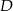 . No i wtedy będzie już łatwo, bo szukane punkty leżą na okręgu o środku
. No i wtedy będzie już łatwo, bo szukane punkty leżą na okręgu o środku 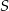 i promieniu
i promieniu 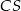 (opisanym na trójkącie
(opisanym na trójkącie 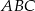 ).
).
Ok, mamy plan działania, to do dzieła. Najpierw równanie prostej  :
:
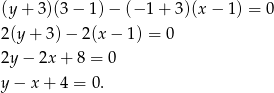
Szkuamy teraz na tej prostej punktu 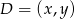 w odległości
w odległości
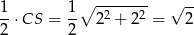
od punktu 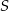 . Mamy zatem układ równań
. Mamy zatem układ równań
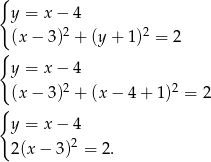
Stąd łatwo wynika, że 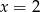 lub
lub 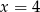 . Pierwszy pierwiastek odrzucamy, bo
. Pierwszy pierwiastek odrzucamy, bo 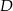 ma być na prawo od
ma być na prawo od 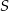 . Mamy zatem
. Mamy zatem 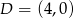 (punkt ten mogliśmy wyliczyć trochę prościej, używając równości wektorów
(punkt ten mogliśmy wyliczyć trochę prościej, używając równości wektorów 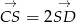 – szczegóły zostawiamy jako ćwiczenie).
– szczegóły zostawiamy jako ćwiczenie).
Równanie prostej 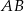 jest postaci
jest postaci 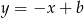 (bo jest ona prostopadła do
(bo jest ona prostopadła do 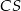 ). Zawiera ona również punkt
). Zawiera ona również punkt 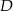 – stąd wyliczymy
– stąd wyliczymy 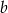 :
:
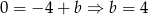
Pozostało teraz znaleźć punkty wspólne prostej 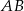 i okręgu:
i okręgu: 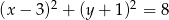 .
.
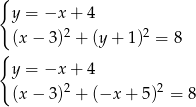
Prowadzi to do równania
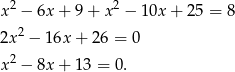
Dalej mamy 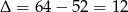 , czyli
, czyli
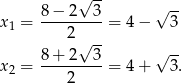
To daje
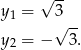
Sposób II
Mając dane współrzędne punktów 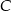 i
i 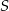 możemy łatwo wyliczyć długość boku trójkąta, bo odcinek
możemy łatwo wyliczyć długość boku trójkąta, bo odcinek 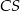 stanowi
stanowi  jego wysokości.
jego wysokości.
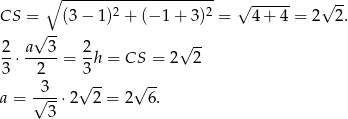
Teraz łatwo napisać dwa równania, które muszą spełniać punkty 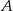 i
i 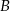 – każdy z nich musi znajdować się w odległości
– każdy z nich musi znajdować się w odległości 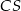 od punktu
od punktu 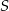 i odległości
i odległości  od punktu
od punktu 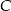 . Otrzymujemy zatem układ równań.
. Otrzymujemy zatem układ równań.
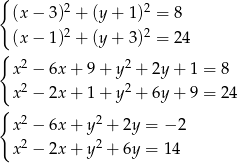
Odejmijmy teraz od drugiego równania pierwsze.
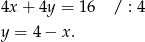
Podstawiamy teraz to wyrażenie do pierwszego równania układu.
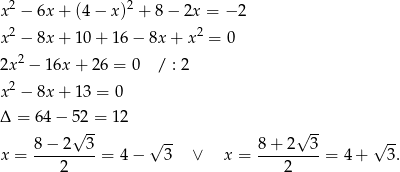
Mamy wtedy odpowiednio 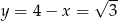 i
i 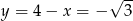 .
.
Odpowiedź: 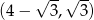 oraz
oraz