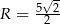/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt

Zadanie nr 6400051

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz promień okręgu opisanego na trójkącie o wierzchołkach 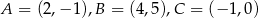A = (2,− 1),B = (4,5),C = (− 1,0) .

Rozwiązanie

Jeżeli naszkicujemy podany trójkąt to rzuca się w oczy, że jest on prostokątny.

PIC

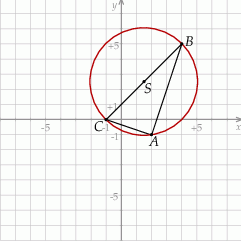
Sprawdźmy to

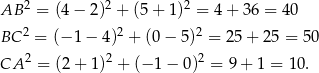
2 2 2 AB = (4 − 2 ) + (5 + 1) = 4 + 3 6 = 40 BC 2 = (− 1 − 4)2 + (0− 5)2 = 25 + 25 = 50 CA 2 = (2+ 1 )2 + (− 1 − 0)2 = 9 + 1 = 10.

Zatem

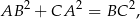
AB 2 + CA 2 = BC 2,

co oznacza, że kąt przy wierzchołku 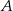A jest prosty. Ponieważ środkiem okręgu opisanego na trójkącie prostokątnym jest środek przeciwprostokątnej, promień tego okręgu jest równy

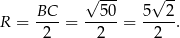
√ --- √ -- R = BC--= --50-= 5--2-. 2 2 2

 
Odpowiedź: √ - R = 52-2

Wersja PDF