Zadanie nr 8374254
Punkty 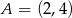 i
i 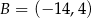 są wierzchołkami trójkąta równoramiennego
są wierzchołkami trójkąta równoramiennego 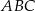 , w którym
, w którym 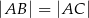 . Wysokość
. Wysokość 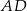 tego trójkąta jest zawarta w prostej o równaniu
tego trójkąta jest zawarta w prostej o równaniu 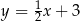 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 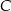 tego trójkąta.
tego trójkąta.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
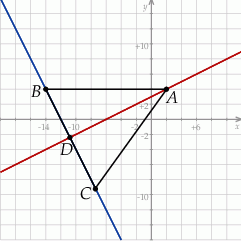
Wysokość 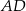 jest prostopadła do boku
jest prostopadła do boku 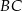 , więc prosta
, więc prosta 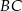 musi mieć równanie postaci
musi mieć równanie postaci 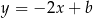 . Współczynnik
. Współczynnik 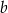 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 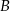 .
.
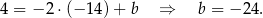
Zatem prosta 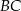 ma równanie
ma równanie 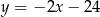 . Punkt
. Punkt 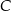 ma więc współrzędne postaci
ma więc współrzędne postaci 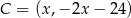 . Pozostało teraz skorzystać z warunku
. Pozostało teraz skorzystać z warunku 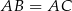 .
.
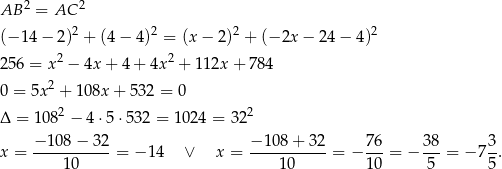
Rozwiązanie 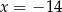 prowadzi do punktu
prowadzi do punktu 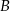 , zatem
, zatem 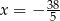 ,
,
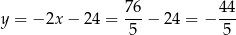
oraz 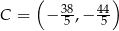 .
.
Odpowiedź: