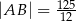/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt

Zadanie nr 9638616

Dodaj do ulubionych
Dodaj do rozwiązanych

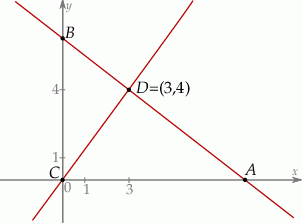
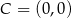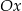Punkt C = (0,0) jest wierzchołkiem trójkąta prostokątnego ABC , którego wierzchołek A leży na osi Ox , a wierzchołek 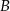B na osi 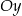Oy układu współrzędnych. Prosta zawierająca wysokość tego trójkąta opuszczoną z wierzchołka 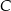C przecina przeciwprostokątną 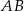AB w punkcie D = (3,4) .

PIC

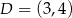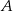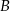Oblicz współrzędne wierzchołków A i B tego trójkąta oraz długość przeciwprostokątnej AB .

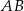Rozwiązanie

Rozpocznijmy od napisania równania wysokości 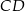CD . Jest to prosta postaci 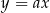y = ax (bo przechodzi przez początek układu współrzędnych). Współczynnik a wyznaczamy podstawiając współrzędne punktu D .

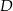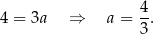
4 = 3a ⇒ a = 4. 3

To oznacza, że współczynnik kierunkowy prostej 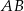AB , która jest prostopadła do 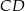CD jest równy 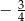− 3 4 . Ma więc ona równanie postaci 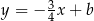y = − 3x + b 4 . Współczynnik 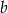b wyznaczamy podstawiając współrzędne punktu D .

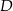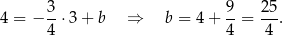
3- 9- 2-5 4 = − 4 ⋅3 + b ⇒ b = 4 + 4 = 4 .

Prosta 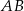AB ma więc równanie 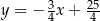y = − 3x + 25 4 4 . W szczególności 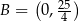( ) B = 0, 25 4 . Aby wyznaczyć współrzędne punktu 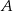A rozwiązujemy równanie

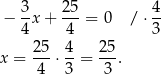
3- 2-5 4- − 4x + 4 = 0 /⋅ 3 2 5 4 25 x = ---⋅ --= --. 4 3 3

Zatem 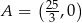(25 ) A = 3 ,0 . Pozostało obliczyć długość odcinka AB .

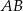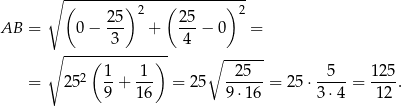
∘ (--------)2---(-------)-2- 25- 25- AB = 0− 3 + 4 − 0 = ∘ ----(--------)- ∘ ------ 1 1 25 5 1 25 = 252 -+ --- = 25 ------= 25 ⋅---- = ----. 9 16 9 ⋅16 3 ⋅4 12

 
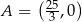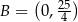Odpowiedź: ( ) A = 253 ,0 , ( ) B = 0, 245 , |AB | = 125 12

Wersja PDF