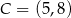Zadanie nr 1110252
Wierzchołki  i
i  trójkąta prostokątnego
trójkąta prostokątnego  leżą na prostej
leżą na prostej 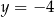 . Okrąg wpisany w ten trójkąt jest styczny do boków
. Okrąg wpisany w ten trójkąt jest styczny do boków 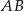 ,
, 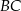 i
i 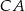 odpowiednio w punktach
odpowiednio w punktach 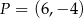 ,
, 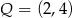 i
i 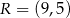 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 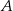 ,
,  i
i  tego trójkąta.
tego trójkąta.
Rozwiązanie
Szkicujemy opisaną sytuację.
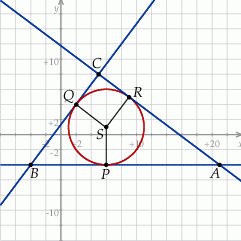
Spróbujemy na początek wyznaczyć środek  okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 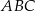 . Punkt
. Punkt  leży na pionowej prostej
leży na pionowej prostej 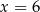 , więc ma współrzędne postaci
, więc ma współrzędne postaci 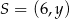 . Ponadto
. Ponadto
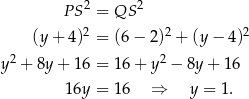
Zatem 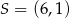 . Napiszemy teraz równania stycznych do okręgu wpisanego w trójkąt
. Napiszemy teraz równania stycznych do okręgu wpisanego w trójkąt  przechodzących przez punkty
przechodzących przez punkty  i
i 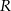 . Są to proste prostopadłe do promieni
. Są to proste prostopadłe do promieni 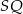 i
i 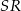 . Wyznaczamy najpierw współczynnik kierunkowy prostej
. Wyznaczamy najpierw współczynnik kierunkowy prostej 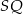 – szukamy prostej w postaci
– szukamy prostej w postaci 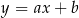 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 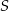 i
i 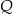 .
.
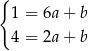
Odejmujemy od pierwszego równania drugie i mamy
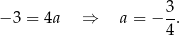
W takim razie prosta 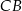 ma równanie postaci
ma równanie postaci 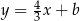 . Współczynnik
. Współczynnik 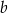 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 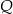 .
.
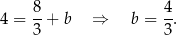
W takim razie prosta 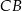 ma równanie
ma równanie 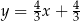 . Szukamy jej punktu wspólnego
. Szukamy jej punktu wspólnego 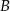 z prostą
z prostą 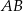
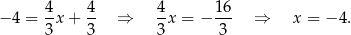
Zatem 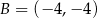 .
.
Korzystamy teraz z informacji o tym, że trójkąt 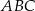 jest prostokątny – to oznacza, że prosta
jest prostokątny – to oznacza, że prosta 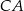 jest prostopadła do
jest prostopadła do 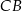 , czyli równoległa do
, czyli równoległa do 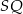 . Ma więc równanie postaci
. Ma więc równanie postaci 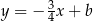 . Współczynnik
. Współczynnik 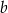 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 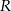 .
.
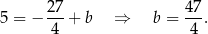
To oznacza, że prosta 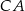 ma równanie
ma równanie 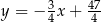 . Wyznaczamy jej punkt wspólny
. Wyznaczamy jej punkt wspólny 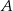 z prostą
z prostą 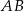 .
.
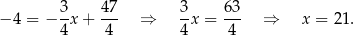
Zatem 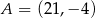 .
.
Pozostało jeszcze wyznaczyć współrzędne punktu 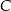 .
.
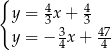
Odejmujemy od pierwszego równania drugie i mamy
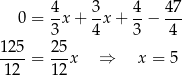
Stąd 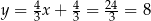 i
i 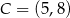 .
.
Odpowiedź: 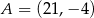 ,
, 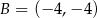 ,
,