/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Prostokątny

Zadanie nr 1392653

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie takiej prostej przechodzącej przez punkt 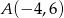A (− 4,6) , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.

Rozwiązanie

Możemy zacząć od rysunku, żeby wiedzieć jakiego wyniku należy się spodziewać.

PIC

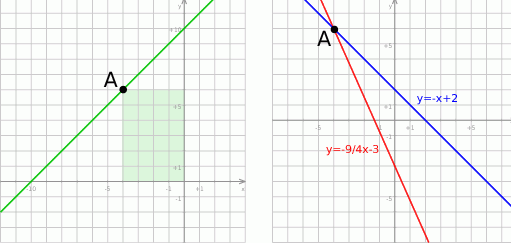
W pierwszej chwili może się wydawać, że są trzy, lub nawet cztery możliwości, ale ponieważ punkt 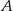A jest odległy od osi o 4 i 6, wariant zielony jest niemożliwy (bo wtedy ten trójkąt zawierałby prostokąt o polu 24, co nie jest możliwe). Należy się więc spodziewać dwóch rozwiązań.

Sposób I

Prostą przechodzącą przez punkt 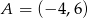A = (− 4,6) możemy zapisać w postaci 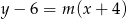y − 6 = m(x + 4 ) , gdzie 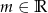m ∈ R ( dokładnie rzecz biorąc jedną prostą w ten sposób pomijamy: pionową, ale ona nie przecina osi 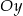Oy , więc nie ma problemu). Wyliczmy punkty przecięcia tej prostej z osiami układu (podstawiamy 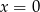x = 0 i y = 0 ).

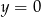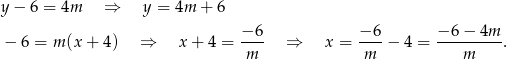
y − 6 = 4m ⇒ y = 4m + 6 − 6 − 6 − 6− 4m − 6 = m (x + 4) ⇒ x+ 4 = ---- ⇒ x = ----− 4 = ---------. m m m

W drugiej równości dzieliliśmy przez 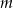m , ale nie ma z tym problemu, bo dla 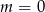m = 0 nasza prosta nie przecina osi 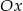Ox . Mamy zatem do rozwiązania równanie

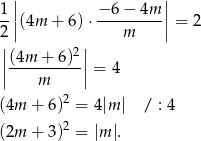
1 || − 6− 4m || --||(4m + 6)⋅ ---------|| = 2 2| | m | (4m + 6)2 | || ----------|| = 4 m (4m + 6)2 = 4|m | / : 4 2 (2m + 3) = |m |.

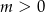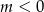Teraz widać, że cztery przypadki, które widzieliśmy na początku odpowiadają w tym równaniu dwóm możliwościom m > 0 i m < 0 . Jak już zauważyliśmy na początku, dla 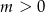m > 0 równanie nie powinno mieć rozwiązań. Sprawdźmy to.

Jeżeli 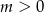m > 0 to mamy

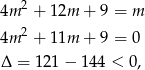
2 4m + 12m + 9 = m 4m 2 + 11m + 9 = 0 Δ = 121 − 144 < 0,

czyli zgodnie z planem.

Jeżeli 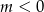m < 0 to mamy

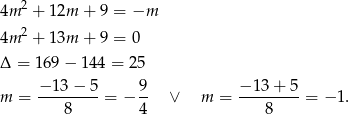
2 4m + 12m + 9 = −m 2 4m + 13m + 9 = 0 Δ = 169 − 144 = 25 − 13 − 5 9 − 13+ 5 m = ---------= − -- ∨ m = ---------= − 1. 8 4 8

Daje to nam odpowiednio proste

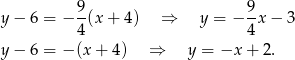
9 9 y− 6 = − --(x+ 4) ⇒ y = − -x − 3 4 4 y− 6 = − (x + 4) ⇒ y = −x + 2.

Sposób II

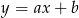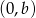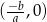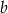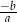Jak już zauważyliśmy, powinniśmy się spodziewać dwóch rozwiązań tak, jak na prawym rysunku. Powiedzmy, że szukana prosta ma równanie y = ax + b . W takim razie jej punkty wspólne z osiami to (0,b) i (−b-,0 ) a . Raz jeszcze patrzymy na prawy rysunek i zauważamy, że w obu sytuacjach liczby b i −b- a mają ten sam znak, czyli równanie z polem możemy zapisać w postaci

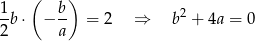
( ) 1b ⋅ − b- = 2 ⇒ b2 + 4a = 0 2 a

(nie potrzeba wartości bezwzględnej). Drugie równanie otrzymamy podstawiając współrzędne punktu 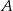A do równania prostej

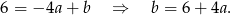
6 = − 4a + b ⇒ b = 6 + 4a.

Wstawiamy tę wartość do poprzedniego równania

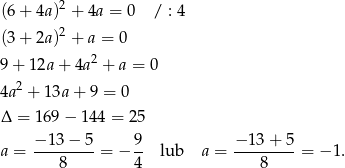
2 (6 + 4a ) + 4a = 0 / : 4 (3 + 2a )2 + a = 0 2 9 + 12a + 4a + a = 0 4a 2 + 1 3a+ 9 = 0 Δ = 169 − 1 44 = 25 − 13 − 5 9 − 13 + 5 a = ---------= − -- lub a = ---------= − 1. 8 4 8

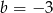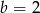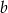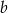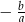Stąd b = − 3 i b = 2 odpowiednio (wybieramy wartości b tak, aby liczby b i b − a miały ten sam znak).  
Odpowiedź: 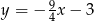y = − 94x− 3 lub y = −x + 2

Wersja PDF