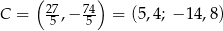/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Prostokątny

Zadanie nr 3194314

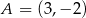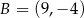W układzie współrzędnych punkty A = (3,− 2) i B = (9,− 4) są wierzchołkami trójkąta 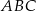ABC . Wierzchołek 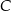C leży na prostej o równaniu 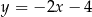y = − 2x− 4 . Oblicz współrzędne punktu 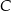C , dla którego kąt 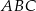ABC jest prosty.

Wersja PDF

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

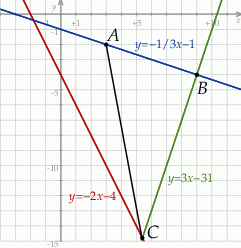
Napiszmy najpierw równanie prostej 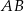AB . Szukamy równania w postaci 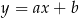y = ax+ b i podstawiamy współrzędne punktów 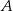A i B .

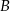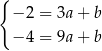
{ − 2 = 3a+ b − 4 = 9a+ b

Odejmujemy od drugiego równania pierwsze i mamy

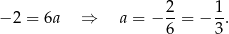
2 1 − 2 = 6a ⇒ a = − --= − -. 6 3

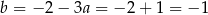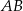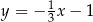Stąd b = − 2 − 3a = − 2 + 1 = − 1 i prosta AB ma równanie 1 y = − 3x − 1 .

Łatwo teraz napisać równanie przyprostokątnej 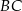BC – jest to prosta prostopadła do 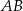AB , więc ma równanie postaci 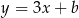y = 3x + b . Ponadto przechodzi ona przez punkt 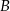B , więc

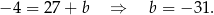
− 4 = 2 7+ b ⇒ b = − 31.

W takim razie prosta 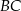BC ma równanie 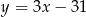y = 3x − 31 . Pozostało wyznaczyć punkt wspólny C tej prostej z daną prostą y = − 2x − 4 .

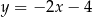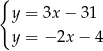
{ y = 3x − 31 y = − 2x− 4

Odejmujemy od pierwszego równania drugie i mamy

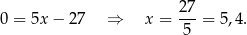
27 0 = 5x − 2 7 ⇒ x = 5--= 5,4.

Stąd

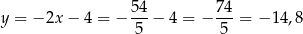
54- 74- y = − 2x − 4 = − 5 − 4 = − 5 = −1 4,8

i 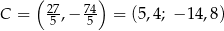( ) C = 275 ,− 745- = (5,4; − 14,8) .  
Odpowiedź: ( ) C = 275 ,− 745- = (5,4; − 14,8)

Wersja PDF