Zadanie nr 3622791
Punkt 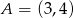 jest wierzchołkiem kąta prostego w równoramiennym trójkącie prostokątnym
jest wierzchołkiem kąta prostego w równoramiennym trójkącie prostokątnym 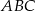 . Przeciwprostokątna tego trójkąta zawiera się w prostej o równaniu
. Przeciwprostokątna tego trójkąta zawiera się w prostej o równaniu 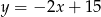 . Wyznacz współrzędne pozostałych wierzchołków trójkąta
. Wyznacz współrzędne pozostałych wierzchołków trójkąta 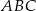 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
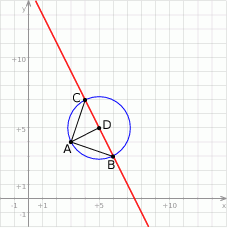
Niech 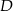 będzie środkiem boku
będzie środkiem boku 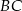 .
.
Sposób I
Długość odcinka 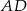 możemy obliczyć ze wzoru na odległość punktu
możemy obliczyć ze wzoru na odległość punktu 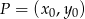 od prostej
od prostej 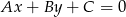 :
:
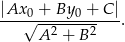
W naszej sytuacji mamy
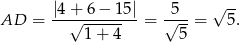
Trójkąt 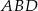 jest równoramienny (bo
jest równoramienny (bo 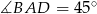 ), więc łatwo obliczyć długość odcinka
), więc łatwo obliczyć długość odcinka 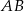 .
.
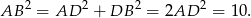
Wystarczy teraz znaleźć punkty danej prostej, które są odległe od 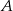 o
o 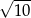 . Szukamy punktu postaci w
. Szukamy punktu postaci w 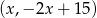 .
.
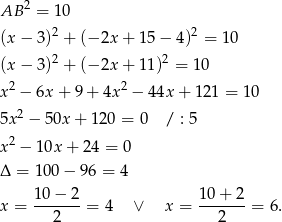
Stąd 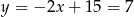 i
i 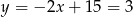 . Zatem współrzędne punktów
. Zatem współrzędne punktów 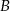 i
i 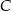 to
to 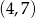 i
i 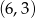 .
.
Sposób II
Zauważmy, że szukane punkty 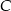 i
i 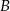 to punkty wspólne danej prostej i okręgu o środku
to punkty wspólne danej prostej i okręgu o środku 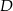 i promieniu
i promieniu 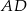 (tak jest, bo środkiem okręgu opisanego na trójkącie prostokątnym jest środek przeciwprostokątnej).
(tak jest, bo środkiem okręgu opisanego na trójkącie prostokątnym jest środek przeciwprostokątnej).
Aby wyznaczyć współrzędne punktu 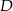 napiszemy równanie prostej
napiszemy równanie prostej 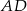 . Ma ona postać
. Ma ona postać 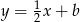 (bo jest prostopadła do
(bo jest prostopadła do 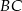 ). Liczbę
). Liczbę 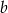 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 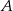 .
.
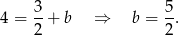
Obliczamy teraz współrzędne punktu 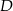 .
.
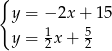
Odejmujemy od drugiego równania pierwsze.
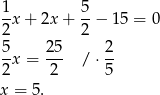
Stąd 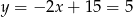 i
i 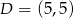 . Obliczmy jeszcze długość odcinka
. Obliczmy jeszcze długość odcinka 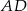 .
.
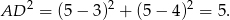
Okrąg o środku 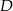 i promieniu
i promieniu 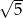 ma równanie
ma równanie
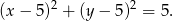
Szukamy punktów wspólnych tego okręgu z daną prostą 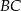 – podstawiamy
– podstawiamy 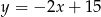 w równaniu okręgu.
w równaniu okręgu.
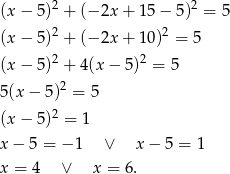
Stąd 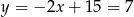 i
i 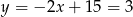 . Zatem współrzędne punktów
. Zatem współrzędne punktów 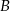 i
i 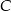 to
to 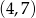 i
i 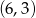 .
.
Odpowiedź: 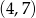 i
i