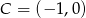/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Prostokątny

Zadanie nr 4728367

Dodaj do ulubionych
Dodaj do rozwiązanych

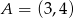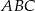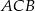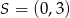Punkt A = (3,4) jest wierzchołkiem trójkąta prostokątnego ABC , o kącie prostym ACB , a S = (0,3) jest środkiem okręgu opisanego na tym trójkącie. Wyznacz współrzędne pozostałych wierzchołków tego trójkąta, wiedząc, że 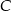C należy do ujemnej części osi Ox .

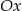Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

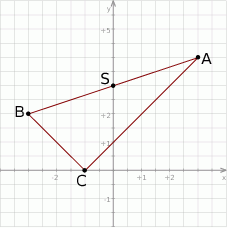
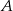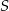Ponieważ środkiem okręgu opisanego na trójkącie prostokątnym jest środek przeciwprostokątnej, a podanych współrzędnych punktów A i S możemy łatwo obliczyć współrzędne drugiego końca przeciwprostokątnej, czyli punktu B .

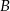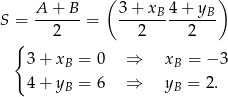
( ) A + B 3 + xB 4 + yB S = -------= -------------- { 2 2 2 3+ xB = 0 ⇒ xB = − 3 4+ yB = 6 ⇒ yB = 2.

Zatem 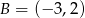B = (−3 ,2) . Pozostało wyznaczyć współrzędne punktu C = (x,0) .

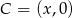Sposób I

Piszemy twierdzenie Pitagorasa w trójkącie 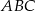ABC .

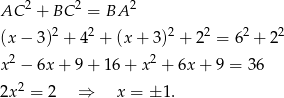
2 2 2 AC + BC = BA (x − 3)2 + 4 2 + (x + 3)2 + 22 = 6 2 + 2 2 x 2 − 6x + 9+ 16+ x2 + 6x + 9 = 36 2 2x = 2 ⇒ x = ± 1.

Ponieważ punkt 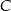C ma należeć do ujemnej części osi 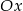Ox , mamy stąd C = (− 1,0) .

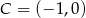Sposób II

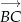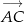Korzystamy z podstawowych własności iloczynu skalarnego – wystarczy sprawdzić, kiedy wektory − → BC i −→ AC są prostopadłe, czyli kiedy ich iloczyn skalarny jest równy 0. Liczymy

−→ −→ BC ∘ AC = 0 [x + 3 ,−2 ]∘[x − 3,− 4] = 0 (x+ 3)(x− 3)+ 8 = 0 2 x − 9+ 8 = 0 ⇒ x = ± 1.

Ponieważ punkt 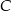C ma należeć do ujemnej części osi 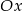Ox , mamy stąd C = (− 1,0) .  
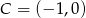Odpowiedź: 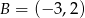B = (− 3,2) , C = (− 1,0)

Wersja PDF