/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Prostokątny

Zadanie nr 4789822

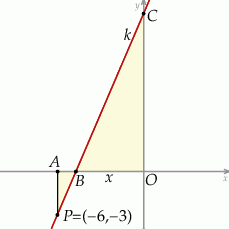
Na rysunku prosta 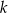k przechodzi przez punkt P (− 6,− 3) .

PIC

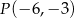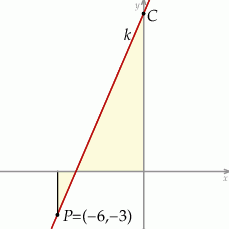
Wiedząc, że stosunek pól zacieniowanych trójkątów prostokątnych jest równy 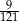1921

  • oblicz pola tych trójkątów;
  • wyznacz równanie prostej k .
Wersja PDF

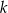Rozwiązanie

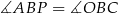  • Jest jasne, że zaznaczone trójkąty są podobne: oba są prostokątne i mają wspólny kąt ostry ∡ABP = ∡OBC .
    PIC

    Ponadto znamy ich skalę podobieństwa:

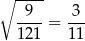
    ∘ ---- 9 3 ----= --- 121 11

    (pole zmienia się jak kwadrat skali). Zatem, przy oznaczeniach z rysunku

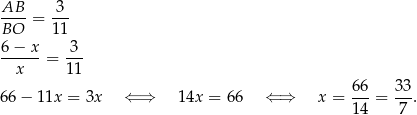
    AB-- -3- BO = 11 6 − x 3 ------= --- x 11 66 − 11x = 3x ⇐ ⇒ 14x = 66 ⇐ ⇒ x = 66-= 33-. 14 7

    Podobnie wyliczamy długość odcinka OC .

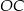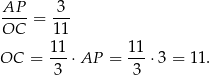
    AP-- -3- OC = 11 11 11 OC = ---⋅AP = ---⋅3 = 11. 3 3

    Możemy teraz policzyć szukane pola.

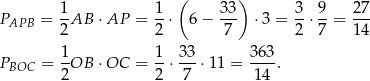
    ( ) 1- 1- 33- 3- 9- 27- PAPB = 2 AB ⋅ AP = 2 ⋅ 6 − 7 ⋅3 = 2 ⋅ 7 = 14 P = 1-OB ⋅ OC = 1-⋅ 33-⋅11 = 3-63. BOC 2 2 7 14

     
    Odpowiedź: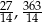 27, 363 14 14

  • Z poprzedniego podpunktu wiemy, że szukana prosta przecina oś 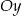Oy w punkcie 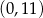(0,11) . Szukamy więc prostej postaci 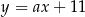y = ax + 11 . Współczynnik a wyliczamy wstawiając do tego równania współrzędne punktu P = (−6 ,−3 ) .
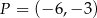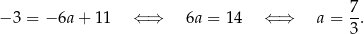
    − 3 = − 6a+ 11 ⇐ ⇒ 6a = 14 ⇐ ⇒ a = 7. 3

     
    Odpowiedź: 7 y = 3x + 1 1

Wersja PDF