Zadanie nr 4790035
Punkty 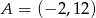 i
i 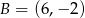 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 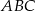 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 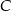 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 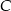 tego trójkąta, wiedząc, że leży on na prostej o równaniu
tego trójkąta, wiedząc, że leży on na prostej o równaniu 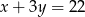 . Sporządź rysunek w prostokątnym układzie współrzędnych. Rozważ wszystkie przypadki.
. Sporządź rysunek w prostokątnym układzie współrzędnych. Rozważ wszystkie przypadki.
Rozwiązanie
Zróbmy najpierw rysunek.
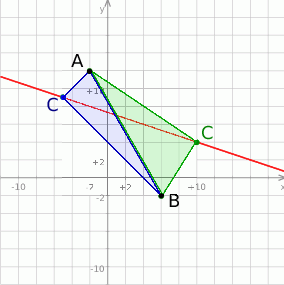
Gołym okiem widać, że będą dwa takie punkty 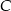 . Jak każde zadanie analityczne, możemy je rozwiązać na wiele różnych sposobów. My zrobimy je na dwa sposoby.
. Jak każde zadanie analityczne, możemy je rozwiązać na wiele różnych sposobów. My zrobimy je na dwa sposoby.
Sposób I
Oznaczymy współrzędne punktu 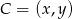 . Napiszemy teraz równania, które pozwolą nam wyliczyć
. Napiszemy teraz równania, które pozwolą nam wyliczyć  i
i 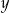 . Aby dostać takie równanie korzystamy z warunku, że wektory
. Aby dostać takie równanie korzystamy z warunku, że wektory
![→ CA = [− 2 − x,12 − y] → CB = [6 − x,− 2 − y]](https://img.zadania.info/zad/4790035/HzadR5x.gif)
mają być prostopadłe.
Przypomnijmy, że wektory ![→v1 = [x1,y1]](https://img.zadania.info/zad/4790035/HzadR6x.gif) i
i ![→v2 = [x2,y2]](https://img.zadania.info/zad/4790035/HzadR7x.gif) są prostopadłe wtedy i tylko wtedy, gdy
są prostopadłe wtedy i tylko wtedy, gdy 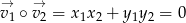 . Mamy zatem
. Mamy zatem
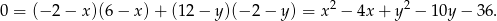
Drugie równanie otrzymujemy z warunku, że punkt 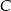 leży na podanej prostej, czyli
leży na podanej prostej, czyli 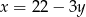 . Uwzględniając to, otrzymujemy
. Uwzględniając to, otrzymujemy
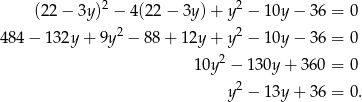
Dalej mamy 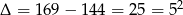 , skąd
, skąd 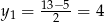 i
i 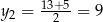 . Z warunku
. Z warunku 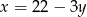 otrzymujemy wtedy
otrzymujemy wtedy 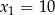 i
i 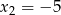 odpowiednio.
odpowiednio.
Sposób II
Ponieważ szukany punkt 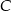 ma być wierzchołkiem trójkąta prostokątnego o przeciwprostokątnej
ma być wierzchołkiem trójkąta prostokątnego o przeciwprostokątnej 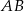 , to musi on leżeć na okręgu o średnicy
, to musi on leżeć na okręgu o średnicy 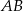 .
.
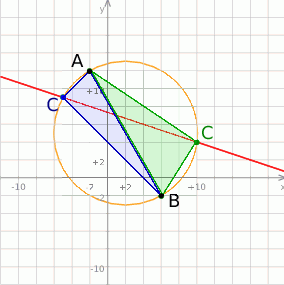
Możemy zatem napisać równanie tego okręgu i znaleźć jego punkty wspólne z daną prostą – będą to szukane punkty. Środek okęgu ma współrzędne
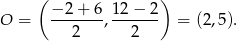
Promień jest równy
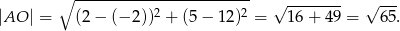
Dostajemy zatem układ równań
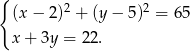
Po wyliczeniu 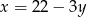 z drugiego równania i podstawieniu do pierwszego, otrzymujemy równanie
z drugiego równania i podstawieniu do pierwszego, otrzymujemy równanie
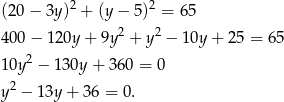
I jesteśmy dokładnie w tej samej sytuacji, co pod koniec poprzedniego sposobu.
Odpowiedź: 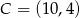 lub
lub