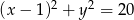Zadanie nr 5306450
W trójkącie prostokątnym 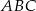 o przeciwprostokątnej
o przeciwprostokątnej 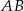 dane są wierzchołki
dane są wierzchołki 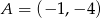 i
i 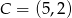 . Punkt
. Punkt 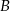 leży na prostej o równaniu
leży na prostej o równaniu 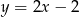 . Wyznacz równanie okręgu opisanego na tym trójkącie.
. Wyznacz równanie okręgu opisanego na tym trójkącie.
Rozwiązanie
Szkicujemy opisaną sytuację.
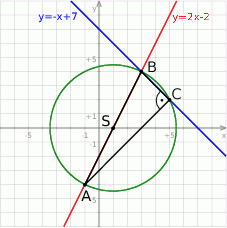
Zauważmy, że znając współrzędne punktów 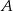 i
i 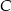 możemy dość łatwo napisać równania prostych
możemy dość łatwo napisać równania prostych 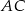 i
i 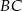 . Pierwsza z nich to po prostu prosta przechodząca przez
. Pierwsza z nich to po prostu prosta przechodząca przez 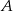 i
i 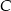 , a druga to prosta prostopadła do
, a druga to prosta prostopadła do 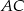 i przechodząca przez
i przechodząca przez 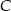 .
.
Zaczynamy od prostej 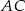 . Szukamy prostej w postaci
. Szukamy prostej w postaci 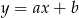 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 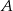 i
i 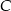 .
.
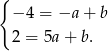
Odejmujemy od drugiego równania pierwsze i mamy 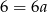 , czyli
, czyli 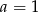 . Współczynnika
. Współczynnika 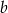 możemy nie obliczać, bo nie jest nam potrzebny.
możemy nie obliczać, bo nie jest nam potrzebny.
Prosta 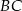 jest prostopadła do
jest prostopadła do 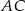 , więc ma postać
, więc ma postać 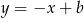 . Współczynnik
. Współczynnik 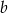 wyznaczamy podstawiając współrzędne punku
wyznaczamy podstawiając współrzędne punku 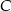 .
.

Zatem prosta 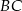 ma równanie:
ma równanie: 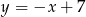 . Szukamy teraz punktu wspólnego
. Szukamy teraz punktu wspólnego 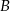 tej prostej z prostą podaną w treści zadania.
tej prostej z prostą podaną w treści zadania.
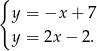
Odejmujemy od drugiego równania pierwsze i mamy

Stąd 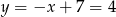 i
i 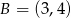 .
.
Okrąg opisany na trójkącie prostokątnym to trójkąt o środku w środku 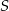 przeciwprostokątnej i promieniu
przeciwprostokątnej i promieniu  równym połowie długości przeciwprostokątnej. W naszej sytuacji mamy
równym połowie długości przeciwprostokątnej. W naszej sytuacji mamy
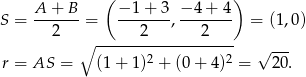
Okrąg opisany na trójkącie  ma więc równanie
ma więc równanie
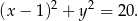
Odpowiedź: