Zadanie nr 5805772
Punkty 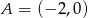 i
i 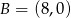 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 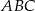 o przeciwprostokątnej
o przeciwprostokątnej 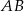 i polu równym 15. Oblicz współrzędne punktu
i polu równym 15. Oblicz współrzędne punktu 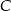 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
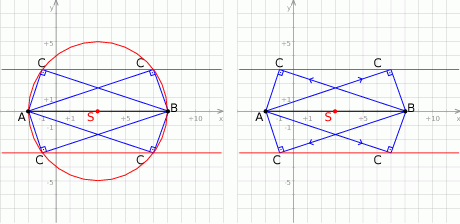
Zauważmy, że znamy długość podstawy trójkąta 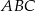 :
:
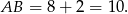
Jeżeli więc 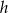 jest długością wysokości opuszczonej na ten bok to z podanego pola mamy
jest długością wysokości opuszczonej na ten bok to z podanego pola mamy
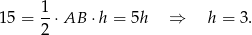
To oznacza, że wierzchołek 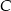 musi leżeć na jednej z prostych
musi leżeć na jednej z prostych 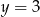 lub
lub 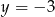 . Jeżeli spojrzymy teraz ponownie na obrazek, to widać, że będą 4 takie punkty
. Jeżeli spojrzymy teraz ponownie na obrazek, to widać, że będą 4 takie punkty 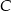 .
.
Sposób I
Skoro trójkąt 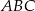 ma być prostokątny, to punkt
ma być prostokątny, to punkt 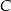 musi leżeć na okręgu o średnicy
musi leżeć na okręgu o średnicy 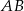 . Nie jest trudno napisać równanie tego okręgu. Jego środek to środek odcinka
. Nie jest trudno napisać równanie tego okręgu. Jego środek to środek odcinka 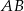 , czyli
, czyli
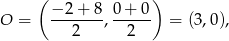
a promień jest równy
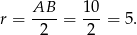
Zatem okrąg o średnicy 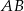 mam równanie
mam równanie
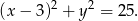
Pozostało wyznaczyć jego punkty wspólne z prostymi 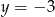 i
i 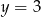 . Zrobimy to za jednym zamachem: podstawiamy
. Zrobimy to za jednym zamachem: podstawiamy 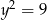 w powyższym równaniu.
w powyższym równaniu.
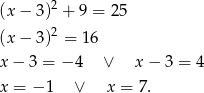
Zatem 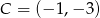 lub
lub 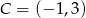 lub
lub 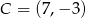 , lub wreszcie
, lub wreszcie 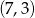 .
.
Sposób II
Szukamy takiego punktu 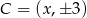 (bo ma leżeć na prostej
(bo ma leżeć na prostej 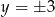 ), aby trójkąt
), aby trójkąt 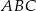 był prostokątny. Zapiszmy twierdzenie Pitagorasa.
był prostokątny. Zapiszmy twierdzenie Pitagorasa.
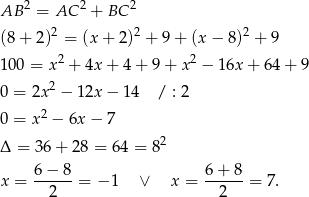
Otrzymujemy w ten sposób te same punkty, co w sposobie I.
Sposób III
Szukamy takiego punktu 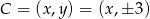 , aby odcinki
, aby odcinki 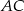 i
i 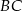 były prostopadłe. Łatwo zapisać ten warunek używając iloczynu skalarnego.
były prostopadłe. Łatwo zapisać ten warunek używając iloczynu skalarnego.
![−A→C ∘B−C→ = 0 [x+ 2,y]∘ [x− 8,y] = 0 (x + 2)(x − 8) + 9 = 0 x2 − 6x − 7 = 0](https://img.zadania.info/zad/5805772/HzadR32x.gif)
Dalej liczmy jak w II sposobie.
Odpowiedź: 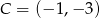 lub
lub 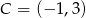 lub
lub 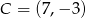 lub
lub