Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 6057712

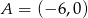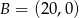Punkty A = (− 6,0) i B = (20,0) są wierzchołkami trójkąta prostokątnego 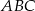ABC o przeciwprostokątnej 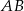AB . Wierzchołek 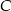C leży na prostej o równaniu 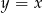y = x . Oblicz współrzędne punktu C .

Wersja PDF
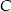Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

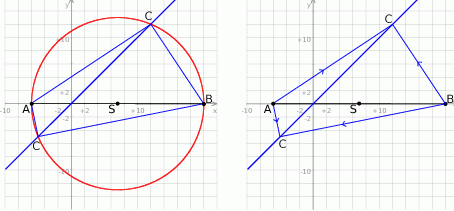
Z obrazka widać, że będą dwa takie punkty 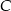C .

Sposób I

Skoro trójkąt 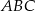ABC ma być prostokątny, to punkt 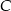C musi leżeć na okręgu o średnicy 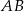AB . Nie jest trudno napisać równanie tego okręgu. Jego środek to środek odcinka 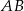AB , czyli

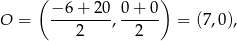
( ) O = −-6+--20, 0-+-0 = (7 ,0), 2 2

a promień jest równy

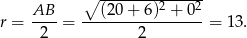
∘ --------------- AB-- ---(20+--6)2 +-02 r = 2 = 2 = 13.

Zatem okrąg o średnicy 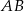AB mam równanie

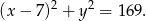
(x − 7)2 + y2 = 169 .

Pozostało wyznaczyć jego punkty wspólne z prostą 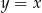y = x – podstawiamy 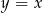y = x w powyższym równaniu.

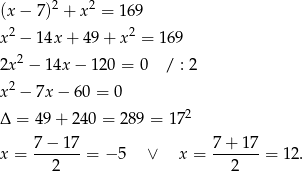
2 2 (x − 7) + x = 1 69 x2 − 14x + 49+ x2 = 169 2 2x − 14x − 120 = 0 / : 2 x2 − 7x − 6 0 = 0 Δ = 49 + 240 = 289 = 17 2 7− 17 7 + 17 x = -------= − 5 ∨ x = -------= 12. 2 2

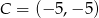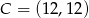Zatem C = (− 5,− 5) lub C = (12,12 ) .

Sposób II

Szukamy takiego punktu 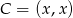C = (x,x) (bo ma leżeć na prostej 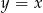y = x ), aby trójkąt 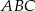ABC był prostokątny. Zapiszmy twierdzenie Pitagorasa.

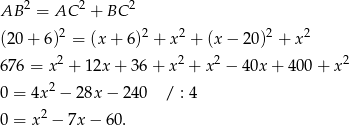
AB 2 = AC 2 + BC 2 (20 + 6)2 = (x + 6 )2 + x 2 + (x − 20 )2 + x 2 2 2 2 2 676 = x + 12x + 36 + x + x − 40x + 4 00+ x 0 = 4x 2 − 28x − 240 / : 4 2 0 = x − 7x − 60.

Dalej liczmy jak w I sposobie.

Sposób III

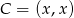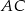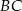Szukamy takiego punktu C = (x,x) , aby odcinki AC i BC były prostopadłe. Łatwo zapisać ten warunek używając iloczynu skalarnego.

−→ −→ AC ∘ BC = 0 [x + 6,x ]∘ [x − 20 ,x] = 0 2 (x+ 6)(x− 20)+ x = 0 x2 − 14x − 120 + x2 = 0 / : 2 x2 − 7x− 60 = 0.

Dalej liczmy jak w I sposobie.  
Odpowiedź: 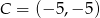C = (− 5,− 5) lub C = (12,1 2)

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!