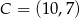Zadanie nr 7353387
Przyprostokątna 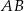 trójkąta prostokątnego
trójkąta prostokątnego 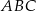 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 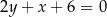 , a środek jego przeciwprostokątnej
, a środek jego przeciwprostokątnej 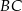 ma współrzędne
ma współrzędne 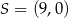 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 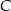 jeżeli
jeżeli 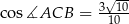 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
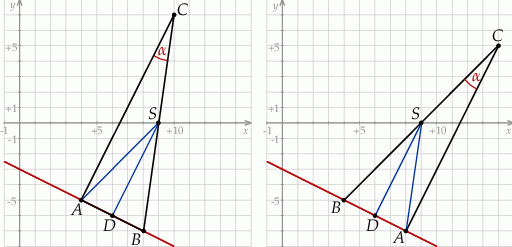
Robiąc obrazek można zauważyć, że możliwe są dwie sytuacje: wszystko zależy od kolejności punktów  i
i  na danej prostej.
na danej prostej.
Po pierwsze zauważmy, że korzystając ze wzoru na odległość punktu od prostej, łatwo jest obliczyć długość przyprostokątnej 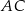 trójkąta
trójkąta 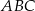 .
.
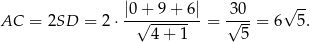
Teraz z podanego cosinusa możemy obliczyć długość przeciwprostokątnej trójkąta 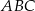 .
.
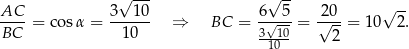
Zauważmy teraz, że w trójkącie prostokątnym środek 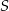 przeciwprostokątnej jest środkiem okręgu opisanego. Tak jest, bo przeciwprostokątna jest średnicą okręgu opisanego. W takim razie punkty
przeciwprostokątnej jest środkiem okręgu opisanego. Tak jest, bo przeciwprostokątna jest średnicą okręgu opisanego. W takim razie punkty 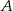 i
i 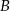 możemy wyznaczyć jako punkty wspólne danej prostej
możemy wyznaczyć jako punkty wspólne danej prostej 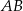 oraz okręgu o środku
oraz okręgu o środku 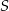 i promieniu
i promieniu 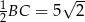 . Rozwiązujemy więc układ równań.
. Rozwiązujemy więc układ równań.
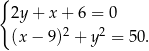
Podstawiamy 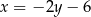 z pierwszego równania do drugiego.
z pierwszego równania do drugiego.
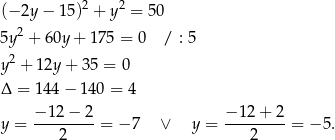
Wtedy odpowiednio 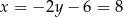 i
i 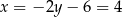 . Zatem punkty
. Zatem punkty  i
i 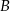 mają współrzędne
mają współrzędne 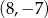 i
i 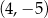 lub odwrotnie. W każdym z przypadku obliczamy współrzędne wierzchołka
lub odwrotnie. W każdym z przypadku obliczamy współrzędne wierzchołka 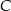 – korzystamy z tego, że
– korzystamy z tego, że 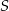 jest środkiem odcinka
jest środkiem odcinka 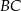 .
.
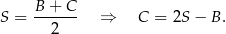
Zatem 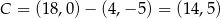 lub
lub 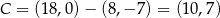 .
.
Odpowiedź: 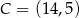 lub
lub