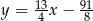Zadanie nr 8877459
Wyznacz równanie symetralnej przeciwprostokątnej trójkąta prostokątnego o wierzchołkach 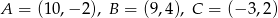 .
.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
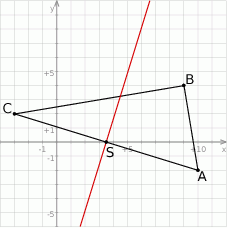
Z rysunku powinno być widać, że przeciwprostokątną jest 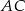 , ale dla pewności sprawdźmy to.
, ale dla pewności sprawdźmy to.
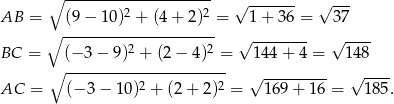
Zatem rzeczywiście 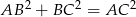 , czyli przeciwprostokątną jest
, czyli przeciwprostokątną jest  . Obliczmy jeszcze współrzędne środka
. Obliczmy jeszcze współrzędne środka  odcinka
odcinka 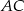 .
.
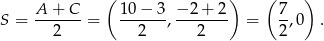
Szukana oś symetrii jest więc symetralną boku  . Jak zwykle w geometrii analitycznej, możemy ją wyznaczyć na różne sposoby.
. Jak zwykle w geometrii analitycznej, możemy ją wyznaczyć na różne sposoby.
Sposób I
Szukana symetralna to zbiór punktów  , które są równo odległe od punktów
, które są równo odległe od punktów 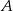 i
i 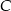 (symetralna odcinka
(symetralna odcinka 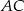 ). Daje to nam równość
). Daje to nam równość
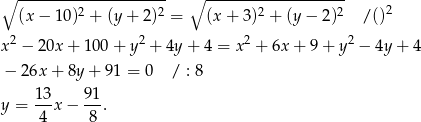
Sposób II
Tym razem napiszemy równanie symetralnej boku 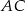 jako prostej prostopadłej do
jako prostej prostopadłej do 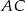 i przechodzącej przez
i przechodzącej przez 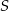 . Najpierw szukamy równania prostej
. Najpierw szukamy równania prostej 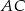 . Szukamy równania w postaci
. Szukamy równania w postaci 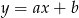 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 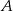 i
i 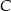 .
.
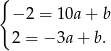
Odejmujemy od pierwszego równania drugie (żeby skrócić 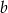 ) i mamy
) i mamy
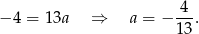
Współczynnika 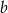 nie obliczamy, bo nie jest nam potrzebny. Symetralna
nie obliczamy, bo nie jest nam potrzebny. Symetralna 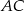 jest prostopadła do
jest prostopadła do 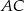 , więc ma równanie postaci
, więc ma równanie postaci 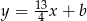 . Współczynnik
. Współczynnik 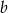 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 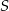 .
.
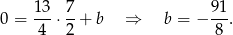
Szukana symetralna ma więc równanie 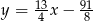 .
.
Sposób III
Szukana prosta jest prostopadła do 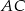 i przechodzi przez
i przechodzi przez 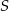 . W takiej sytuacji bardzo wygodny jest wzór na równanie prostej prostopadłej do wektora
. W takiej sytuacji bardzo wygodny jest wzór na równanie prostej prostopadłej do wektora ![→ v = [p,q]](https://img.zadania.info/zad/8877459/HzadR34x.gif) i przechodzącej przez punkt
i przechodzącej przez punkt 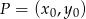
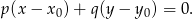
W naszej sytuacji mamy ![→ →v = AC = [− 13,4]](https://img.zadania.info/zad/8877459/HzadR37x.gif) i
i 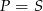 , co daje równanie
, co daje równanie
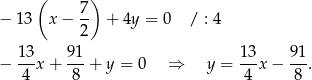
Odpowiedź: