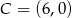Zadanie nr 9420008
Punkty 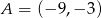 i
i 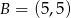 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 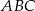 , w którym
, w którym 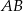 jest przeciwprostokątną. Wyznacz współrzędne wierzchołka
jest przeciwprostokątną. Wyznacz współrzędne wierzchołka 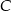 wiedząc, że leży on na osi
wiedząc, że leży on na osi 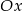 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
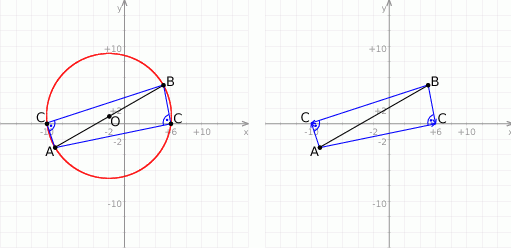
Z obrazka widać, że będą dwa takie punkty 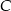 .
.
Sposób I
Skoro trójkąt 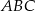 ma być prostokątny, to punkt
ma być prostokątny, to punkt 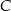 musi leżeć na okręgu o średnicy
musi leżeć na okręgu o średnicy 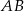 . Nie jest trudno napisać równanie tego okręgu. Jego środek to środek odcinka
. Nie jest trudno napisać równanie tego okręgu. Jego środek to środek odcinka 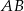 , czyli
, czyli
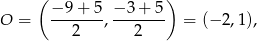
a promień jest równy
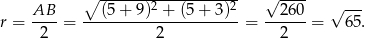
Zatem okrąg o średnicy 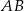 mam równanie
mam równanie
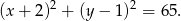
Pozostało wyznaczyć jego punkty wspólne z osią  – podstawiamy
– podstawiamy  .
.
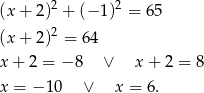
Zatem 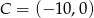 lub
lub 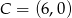 .
.
Sposób II
Szukamy takiego punktu 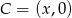 , aby odcinki
, aby odcinki 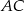 i
i  były prostopadłe. Na mocy twierdzenia Pitagorasa musimy rozwiązać równanie
były prostopadłe. Na mocy twierdzenia Pitagorasa musimy rozwiązać równanie
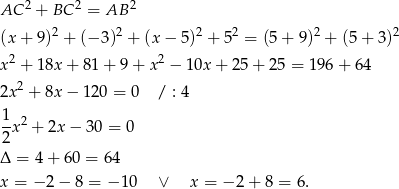
Zatem 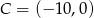 lub
lub 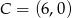 .
.
Sposób III
Szukamy takiego punktu 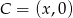 , aby odcinki
, aby odcinki 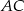 i
i 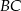 były prostopadłe. Łatwo zapisać ten warunek używając iloczynu skalarnego.
były prostopadłe. Łatwo zapisać ten warunek używając iloczynu skalarnego.
![−AC→ ∘ −B→C = 0 [x + 9,3]∘ [x − 5,− 5] = 0 (x + 9)(x − 5 )− 1 5 = 0 x 2 + 9x − 5x − 45− 15 = 0 2 x + 4x − 6 0 = 0 Δ = 16 + 240 = 256 = 16 2 x = −-4−--16-= − 1 0 ∨ x = −-4-+-16-= 6. 2 2](https://img.zadania.info/zad/9420008/HzadR24x.gif)
Zatem 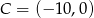 lub
lub 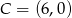 .
.
Odpowiedź: 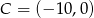 lub
lub