Zadanie nr 9837304
Punkt 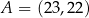 jest wierzchołkiem trójkąta prostokątnego o polu
jest wierzchołkiem trójkąta prostokątnego o polu 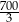 . Prosta
. Prosta 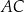 zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną
zawiera przeciwprostokątną tego trójkąta, a prosta zwierająca przyprostokątną 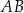 ma równanie
ma równanie 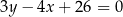 . Środek okręgu wpisanego w trójkąt
. Środek okręgu wpisanego w trójkąt 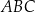 ma współrzędne
ma współrzędne 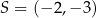 . Oblicz współrzędne wierzchołków
. Oblicz współrzędne wierzchołków 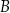 i
i 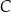 tego trójkąta.
tego trójkąta.
Rozwiązanie
Szkicujemy opisaną sytuację.
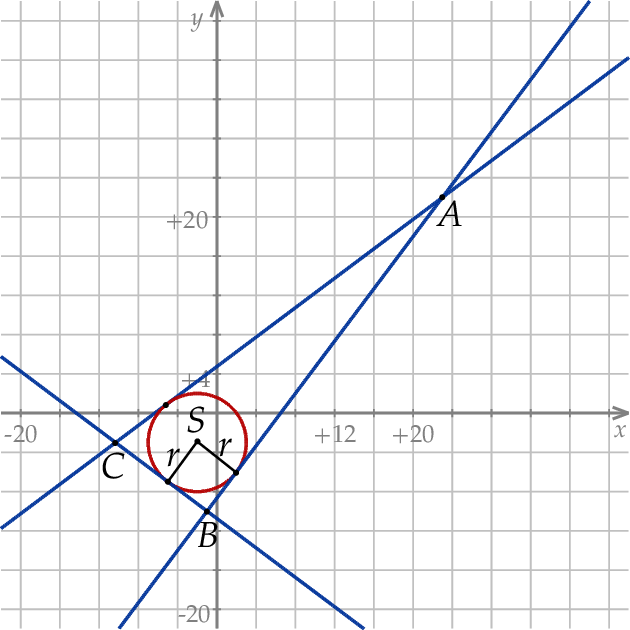
Zauważmy na początek, że łatwo jest obliczyć promień  okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 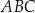 – jest to po prostu odległość punktu
– jest to po prostu odległość punktu 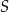 od prostej
od prostej 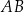 .
.
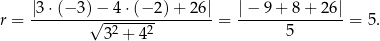
Spróbujemy teraz napisać równanie prostej 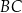 . Jest ona prostopadła do prostej
. Jest ona prostopadła do prostej 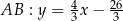 , więc ma równanie postaci
, więc ma równanie postaci 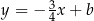 oraz jej odległość od
oraz jej odległość od 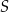 też musi być równa
też musi być równa 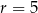 . Aby sprawdzić kiedy tak będzie, zapiszmy jej równanie w postaci ogólnej:
. Aby sprawdzić kiedy tak będzie, zapiszmy jej równanie w postaci ogólnej: 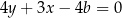 i ponownie korzystamy ze wzoru na odległość punktu od prostej.
i ponownie korzystamy ze wzoru na odległość punktu od prostej.
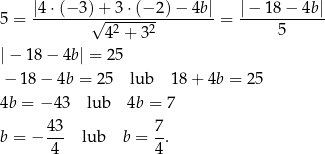
Zauważmy teraz, że w przypadku 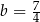 prosta
prosta 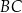 miałaby równanie
miałaby równanie 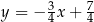 i wtedy punkty
i wtedy punkty 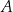 i
i 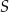 leżałyby po różnych stronach tej prostej. Dokładniej,
leżałyby po różnych stronach tej prostej. Dokładniej,
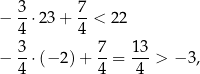
czyli punkt 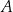 leżałby powyżej, a punkt
leżałby powyżej, a punkt 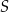 poniżej prostej
poniżej prostej 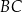 , a to jest niemożliwe. Zatem
, a to jest niemożliwe. Zatem 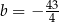 i prosta
i prosta 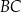 ma równanie
ma równanie 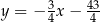 . Szukamy teraz punktu wspólnego
. Szukamy teraz punktu wspólnego 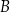 tej prostej i danej prostej
tej prostej i danej prostej 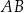 .
.
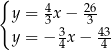
Odejmujemy od pierwszego równania drugie i mamy
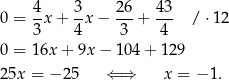
Stąd 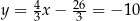 i
i 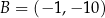 .
.
W tym momencie musimy wykorzystać podaną informację o polu trójkąta 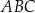
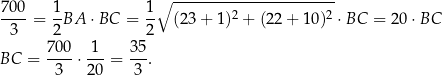
Pozostało teraz wyznaczyć taki punkt 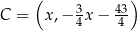 na prostej
na prostej 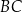 , dla którego
, dla którego 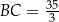 .
.
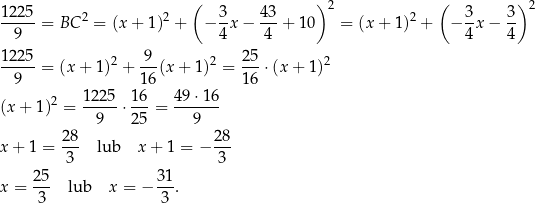
Mamy wtedy 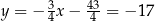 lub
lub 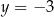 odpowiednio. Aby ustalić, który z tych punktów jest szukanym punktem
odpowiednio. Aby ustalić, który z tych punktów jest szukanym punktem 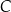 , sprawdzamy, który z nich leży powyżej prostej
, sprawdzamy, który z nich leży powyżej prostej 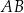 (bo
(bo 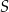 leży powyżej tej prostej).
leży powyżej tej prostej).
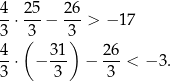
W takim razie 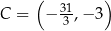 .
.
Odpowiedź: 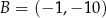 ,
,