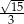Zadanie nr 2858216

Dany jest wierzchołek trójkąta równobocznego 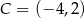C = (− 4,2) . Bok 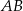zawarty jest w prostej o równaniu 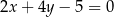2x + 4y− 5 = 0 . Wyznacz długość boku tego trójkąta.

Rozwiązanie

Zaczynamy od rysunku

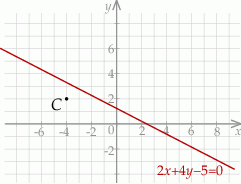
Ponieważ bok 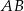zawiera się w podanej prostej, więc odległość punktu 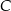od tej prostej będzie równa wysokości szukanego trójkąta

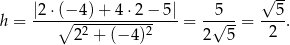
√ -- |2-⋅(−-4)+--4⋅-2−--5| --5-- --5- h = ∘ -2--------2 = 2√ 5-= 2 . 2 + (− 4)

Ze wzoru na wysokość trójkąta równobocznego wyznaczamy długość boku

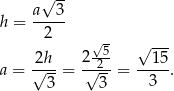
√ -- h = a--3- 2 √- -5- √ --- a = √2h-= 2√2--= --15. 3 3 3

Odpowiedź: √ -- --15 3

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz