/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoboczny

Zadanie nr 2930917

Dodaj do ulubionych
Dodaj do rozwiązanych

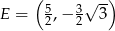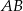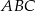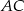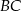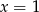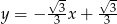Punkt (5 3 √ -) E = 2,− 2 3 jest środkiem boku AB trójkąta równobocznego ABC , a boki AC i BC tego trójkąta są zawarte odpowiednio w prostych o równaniach x = 1 i √3- √3- y = − 3 x + 3 . Wyznacz współrzędne wierzchołków tego trójkąta.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

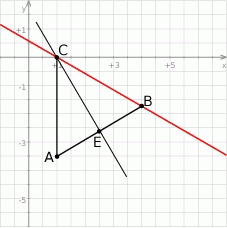
Wyznaczamy najpierw współrzędne punktu wspólnego 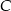C podanych prostych 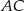AC i BC .

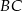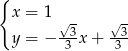
{ x = 1 √-3 √-3 y = − 3 x + 3

Mamy stąd 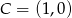C = (1,0) . Piszemy teraz równanie wysokości 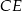CE trójkąta. Szukamy prostej w postaci 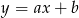y = ax + b i podstawiamy współrzędne punktów 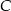C i E .

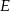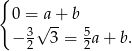
{ 0 = a+ b 3√ -- 5 − 2 3 = 2 a+ b .

Odejmujemy od drugiego równania pierwsze i mamy

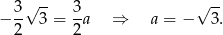
√ -- √ -- − 3- 3 = 3a ⇒ a = − 3. 2 2

Współczynnika 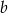b nie wyznaczamy, bo nie jest nam potrzebny. Piszemy teraz równanie prostej 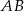AB – jest ona prostopadła do 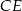CE , więc ma postać

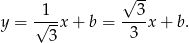
√ -- 1 3 y = √--x + b = -3-x + b. 3

Współczynnik 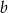b wyznaczamy podstawiając współrzędne punktu E .

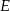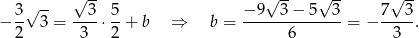
√ -- √ -- √ -- √ -- √ -- − 3- 3 = --3-⋅ 5+ b ⇒ b = −-9--3−--5--3-= − 7--3. 2 3 2 6 3

Prosta 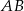AB ma więc równanie 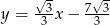√ 3 7√ 3 y = -3-x − --3- . Punkt wspólny tej prostej z prostą 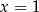x = 1 to

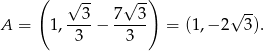
( √ -- √ -) --3- 7--3- √ -- A = 1, 3 − 3 = (1,− 2 3).

Współrzędne punktu 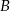B wyznaczamy korzystając z tego, że 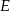E jest środkiem odcinka AB .

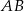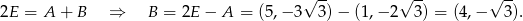
√ -- √ -- √ -- 2E = A + B ⇒ B = 2E − A = (5 ,− 3 3)− (1 ,−2 3) = (4,− 3).

 
Odpowiedź: √ -- √ -- A = (1,− 2 3), B = (4,− 3), C = (1,0)

Wersja PDF